Leseprobe
Page 12
3.2) Credibility-Schätzer
3.2.1) Der einstufige Fall (s=1) :
Der einstufige Fall wurde bereits in der Vorlesung behandelt (siehe „Kremer:
Versicherungsmathematik, Hamburg 1998“ , Seite 57-65). Er sei dennoch an dieser Stelle kurz
wiederholt.
Für den einstufigen Fall werden die Annahmen (3) und (4) nicht benötigt. Das Problem besteht also
θ = ) ( b b nun darin, zu schätzen, wobei angenommen sei, daß die Parameter (2.6) - (2.8) bekannt
i i 1 1
sind. Um die Notation zu wahren, werden einfach alle Indizes weggelassen und man betrachtet die
Gleichung
E(x n x 1 | θ) = Y n x q b q x 1 (θ) (3.3)
mit den Parametern
β q x 1 = E[b(θ)] Λ q x q = Var[b(θ)] Φ n x n = E[Var(x | θ)] , , (3.4)
Man erhält folgenden Satz:
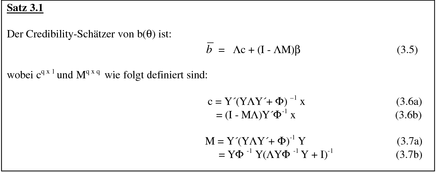
Die sogenannte Credibility-Matrix ist dabei definiert gemäß:
Z =
ΛM
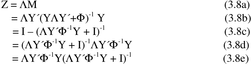
Für den Fall, daß für die Anzahl der Beobachtungen gilt n ≥ q und Y vollen Rang q hat, so läßt sich
b in der Form eines gewichteten Mittels darstellen:
Page 21
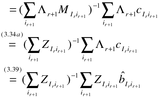
Anmerkung 1: Die Formel (3.35a) ist also eine Folgerung aus (3.34a) und (3.39).
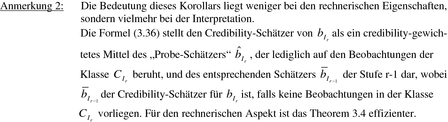
![]()
3.3) Das LB-Risiko
b läßt sich darstellen gemäß: Das LB-Risiko bei der Schätzung von
I r
tr ∆ = ρ ) ( W (3.41)
I I r r
(siehe R.Norberg „Empirical Bayes Credibility“ in Scand. Actuarial Journal 1980, S.181)
∆ die LB-Risikomatrix symbolisiert, gegeben durch
wobei tr die Spur bedeutet und
I r
′ ′ − − = ∆ 1 ) , ( )] ( )[ , ( ) ( b x Cov x Var x b Cov b Var (3.42)
I I I I I I I 1 1 r r r r r
- Arbeit zitieren
- Sven Bartels (Autor:in), 2000, Hierarchische Credibility-Theorie, München, GRIN Verlag, https://www.grin.com/document/98969
Kostenlos Autor werden






















Kommentare