Hohlraumresonanzen Quader/Kugel

Page 3

1 Grundlagen

1.1 Akustik im Allgemeinen

Akustik ist die Lehre vom Schall. Sie befasst sich mit mechanischen Schwingungen im Frequenzbereich zwischen 16 Hz (untere H¨ orgrenze) und 20 kHz (obere H¨ orgrenze), die sich in Festk¨ orpem, Fl¨ ussigkeiten und Gasen in Form von Druckschwankungen ausbreiten. Man unterscheidet: Ton, Klang, Ger¨ ausch und Knall

• Ton (reiner Ton): Ist eine Sinusschwingung

• Klang: ¨ Uberlagerung mehrerer T¨ one. Es ¨ uberlagern sich mehrere sinusf¨ ormi-

ge Schwingungen zu einer nicht sinusf¨ ormigen Schwingung. Der Ton mit der niedrigsten Frequenz bestimmt die Tonh¨ ohe der gesamten Schallempfindung, die anderen (Obert¨ one) verursachen den Eindruck der Klangfarbe.

• Ger¨ ausch: Ist eine unregelm¨ aßige Schwingung, ein Gemisch aus sehr vielen Frequenzen etwa gleicher Gr¨ oßenordnung.

• Knall: Ist ein kurzzeitiger und starker Schalleindruck.

1.1.1 Der Schall

Die Ausbreitung des Schalls erfolgt in der Form von mechanischer L¨ angswellen ( Longitudinalwellen). Die Phasengeschwindigkeit dieser Wellen, meist als Schallgeschwindigkeit c bezeichnet, h¨ angt nur von den mechanischen Eigenschaften des Mediums, nicht aber von der Frequenz der Wellen ab.

^E • Schallgeschwindigkeit in Festk¨ orpem: c =

ξ

K ¹ • Schallgeschwindigkeit in Fl¨ ussigkeiten: c = =

^{ξ χ·ξ} √

^χ·p • Schallgeschwindigkeit in Gasen: c = χ · R · T , bzw. c =

ξ

wobei:

E Elastizit¨ atsmodul eines Stabes K Kompressionsmodul der Fl¨ ussigkeit χ Adiabatenexponent p Gasdruck R Gaskonstante T Gastemperatur

ξ Dichte des jeweiligen Mediums ⇒ die Schallgeschwindigkeit ist temperaturabh¨ angig

Setzt man die Zahlenwerte f¨ ur trockene Luft ( durch den Gehalt an Wasserdampf

Page 4

¨ andert sich die Schallgeschwindigkeit nur unmerklich ) von 0 ^◦ C ein, so erh¨ alt man:

c 0 =

1.1.2 ¨ Uberlagerung von Schallwellen

F¨ ur die ¨ Uberlagerung (Interferenz) von Schallwellen gelten die gleichen Gesetzm¨ aßigkeiten wie f¨ ur alle anderen Wellenarten. Hier sind nur die wichtigsten F¨ alle nochmals genannt:

• Ausl¨ oschung: Zwei Schallwellen gleicher Ausbreitungsrichtung, Frequenz und Amplitude l¨ oschen sich aus, wenn sie einen Gangunterschied von

besitzen. Bei ungleicher Amplitude ergibt sich eine Schw¨ achung.

• Verst¨ arkung: Zwei Schallwellen gleicher Ausbreitungsrichtung, Frequenz und Amplitude verst¨ arken sich zu doppelt so großer Elongation bei einem Gangunterschied von

k · λ ; k = 0, 1, 2, . . .

Bei ungleicher Amplitude ergibt sich unter gleicher Bedingung eine Addition der Elongationen.

• Schwebung: Die ¨ Uberlagerung zweier Schallwellen gleicher Ausbreitungsrichtung ergibt bei geringer Frequenzdifferenz eine Schwebung. Die Amplitude der resultierenden Welle nimmt periodisch zu und ab.

• Stehende Welle: Eine stehende Welle entsteht, wenn zwei Schallwellen gleichzeitig in entgegengesetzte Richtung durch das Medium laufen. Vorausgesetzt sie stimmen in Amplitude, Frequenz und Wellenl¨ ange ¨ uberein.

Page 5

1.2 Schwingungen

Schwingungen sind allgemein solche Zustands¨ anderungen eines Systems, deren zeitlicher Ablauf sich nach einem Zeitintervall T stets reproduziert. Periodisch nennt man eine Schwingung, wenn diese Zeitintervalle jeweils identisch sind. Es gilt:

φ(t + n · T ) = φ(t) wobei n eine ganze Zahl ist.

Die Bewegung eines Punktes einer periodischen Schwingung l¨ aßt sich nach einer Projektion als eine Kreisbewegung mit zeitabh¨ angigen Radius beschreiben, wobei die Kreisbahn senkrecht zur Ebene steht.

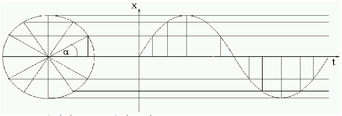
Abb.3 Die harmonische Schwingung als gleichf¨ ormige Kreisbewegung ( siehe Gerthsen, Vogel, 8.16) Hierbei gilt:

r(t) = r(t + T ).

Man kann daher einer periodischen Schwingung eine Winkelgeschwindigkeit ω zuordnen:

ω =

Die Amplitude ist die gr¨ oßte Elongation, die w¨ ahrend einer Schwingung auftritt. Schwingungen lassen sich mit Hilfe von Differentialgleichungen beschreiben. Man unterscheidet dabei zwischen:

1.2.1 Harmonischen Schwingungen

Schwingungen heißen harmonisch, wenn r(t) sinus- oder cosinusf¨ ormig verl¨ auft. Harmonische Schwingungen treten auf, wenn die r¨ ucktreibende Kraft proportional zur Auslenkung ist. Die Differentialgleichung f¨ ur harmonische Schwingungen lautet: d ² φ(t)

dt 2 + ω 2 0 φ(t) = 0 (1)

Deren L¨ osung eine Sinus-Funktion ist:

φ(t) = A · sin(ω 0 t + α) (2)

Page 6

1.2.2 Ged¨ ampfte Schwingungen

Freie Schwingungen zeigen im realen Fall eine zeitlich abnehmende Amplitude. Sie sind ged¨ ampft. Die Differentialgleichung lautet:

Deren L¨ osung im Schwingfall ist:

φ(t) = Ae ^−δt sin(ω g t + α) (4)

ω 2 0 + δ ² , A = Amplitude von φ.) (Mit δ = D¨ ampfungskonstante, ω g =

Der Ausdruck Ae ^−δt beschreibt die Amplitude der ged¨ ampften Schwingung als Funktion der Zeit. Die Abnahme der Amplitude ist durch Reibung bedingt. Der Zeitraum, in dem die Schwingungsamplitude auf ihren e - ten Teil abgeklungen ist, wird als Abklingdauer τ = ¹ bezeichnet. Unged¨ ampfte Schwingungen kommen

δ

in der Natur nicht vor, sondern nur ged¨ ampfte. Ist die Schwingungsdauer T klein gegen¨ uber der Abklingdauer τ , so darf man schwach ged¨ ampfte Schwingungen als harmonische betrachten.

1.2.3 Erzwungene Schwingungen

Schwingungen unter Einwirkung ¨ außerer Kr¨ afte oder Drehmomente nenn man erzwungene Schwingungen:

Deren L¨ osungen lauten:

φ(t) = Ae ^−δt sin(ω F t − γ) (6)

(F (t) = F 0 cos(ω F t) entspricht der von außen am System angreifende Ktaft; γ = Phasenverschiebung zwischen φ(t) und F (t))

Die Amplitude berechnet sich aus:

A =

(Mit m = Masse des schwingenden K¨ orpers; ω = Eigenfrequenz des Oszillators; ω F = Frequenz der anregenden Kraft)

Die Amplitude einer erzwungenen Schwingung ist eine Funktion der Frequenz ω F der anregenden Kraft. Wie man aus Gleichung (7) erkennen kann, wird die

Page 7

Amplitude maximal, wenn die Frequenz ω F mit der Eigenfrequenz ω des Oszil-lators ¨ ubereinstimmt. In diesem Fall spricht man von Resonanz. Der Grund f¨ ur die zeitlich konstante Amplitude ist die Kompensation der am System wirkenden Reibungskr¨ afte durch die ¨ außere, anregende Kraft. Das heißt, diese Schwingung wird daher nicht ged¨ ampft. F¨ ur die Geschwindigkeit v des Oszillators gilt folgender Zusammenhang:

v =

(Wobei man v 0 = ω F A als Geschwindigkeitsamplitude bezeichnet.)

1.3 Wellen

Eine Welle ist die zeitliche, meist periodisch r¨ aumlich sich ausbreitenden Zu-stands¨ anderungen physikalischer Gr¨ oßen.

Solche Ph¨ anomene findet man beim Druck in einem Gas, bei der Verformung einer Feder, die mit anderen gekoppelt ist, bei Belastungen in einem Festk¨ orper (z.B. Scher- , Schubspannungen etc.), sowie bei elektromagnetischen Feldern. Zur Erzeugung von Wellen muß Arbeit verrichtet werden. Die Wellenausbreitung erfolgt ohne Massentransport, dagegen werden mechanische Erhaltungsgr¨ oßen wie Energie und Impuls ¨ ubertragen.

Hat die physikalische Gr¨ oße vektoriellen Charakter ( Feldst¨ arke, Schwingung eines Teilchens um seine Ruhelage ) so muss unterschieden werden, ob die Schwingung in Ausbreitungsrichtung ( Longitudinal - Welle ) oder senkrecht dazu (Transversal - Welle ) erfolgt. Ein Beispiel f¨ ur Transversalwellen w¨ are eine elektromagnetische Welle, f¨ ur die longitudinale Ausbreitung eine Schallwelle. Eine Welle ψ( r, t) l¨ asst sich durch die L¨ osung der Wellengleichung, einer partiellen Differentialgleichung zweiter Ordnung, beschreiben. Die Wellengleichung lautet:

∆ψ =

(Mit c = Ausbreitungsgeschwindigkeit; ∆ = Laplaceoperator; r = Ortsvektor)

Eine L¨ osung dieser Wellengleichung f¨ ur den eindimensionalen Fall ist die harmonische Welle:

t

ψ(x, t) = A · sin 2π

(Mit A = Amplitude; T = Schwingungsdauer; λ = Wellenl¨ ange; t = Zeit; x = Abstand zur Quelle)

Page 8

1.3.1 Herleitung der Wellengleichung

Eine Schallwelle ist mit einer r¨ aumlichen und zeitlichen Schwankung der Dichte, des Druckes und der Temperatur verbunden.

Die Herleitung erfolgt anhand der Theorie von Schallfeldern. Eine Schallwelle wird durch drei Gr¨ oßen beschrieben: 1.) Druckschwankungen p = p − + p ^∼ 2.) Dichteschwankungen ρ = ρ − + ρ ^∼ 3.) Schallschnelle v = v − + v ∼

(p − , ρ − , v − sind die zeitunabh¨ angigen Mittelwerte, die auch ohne Schallfeld vor-handen sind. p ∼ , ρ ∼ , v ∼ sind die ver¨ anderlichen Schallfeldgr¨ oßen Wechseldruck, Wechseldichte und Wechselschnelle. Die Schallschnelle v entspricht der Teilchengeschwindigkeit, und ist nicht zu verwechseln mit der Ausbreitungsgeschwindigkeit der Welle.)

Das Schallfeld wird durch eine skalare und eine vektorielle Gr¨ oße (meist durch den Druck und die Schnelle) beschrieben, im Gegensatz zur elektromagnetischen Welle, die durch zwei vektorielle Gr¨ oßen, n¨ amlich der elektrischen und der magnetischen Feldst¨ arke.

Zur Beschreibung von Schallfeldern werden drei grundlegende Gleichungen herangezogen:

Die ersten zwei Gleichungen sind die hydrodynamischen Grundgleichungen. Die dritte Gleichung wird als Zustandsgleichung der Materie bezeichnet.

1.) Eulersche Grundgleichung ρ 2.) Kontinuit¨ atsgleichung 3.) Adiabatengesetz

Die Eulersche Grundgleichung ist das Pendant zum zweiten Newtonschen Axiom F = m · a. Sie beschreibt die Beschleunigung der in einem Volumenelement ent haltenen Masse, die durch eine Kraft hervorgerufen wird. Die Kontinuit¨ atsgleichung dr¨ uckt die Massenerhaltung aus. Das Adiabatengesetz erl¨ autert den Zusammenhang zwischen dem Druck p und der Dichte ρ des Mediums. Es gilt jedoch nur, wenn die Zustands¨ anderungen eines Gases nicht isotherm (Temperatur T = const.), sondern adiabatisch verlaufen, was bei einer Schallwelle der Fall ist.

Zur Herleitung der Wellengleichung werden folgende Annahmen gemacht:

1.) Die Wechselgr¨ oßen sind stets klein gegen¨ uber den Gleichgr¨ oßen. 2.) Vernachl¨ assigung der r¨ aumlichen Geschwindigkeits-(Schnelle-) ¨ anderung gegen¨ uber ihrer zeitlichen ¨ Anderung ^∂v ) v wird

∂t

nicht beachtet.

Es folgt f¨ ur die Eulersche Gmndgleichung:

∂ v

p − ρ −

∂t

Page 9

Die Kontinuit¨ atsgleichung ergibt sich zu:

ρ − div v ∼ = −

F¨ ur eine ebene Welle, die in den Schallfeldgr¨ oßen nur von einer Ortskoordinate, z.B. x abh¨ angt, erh¨ alt man mit p − = c ² · p ∼ :

ρ −

Die erste Gleichung wird partiel nach dem Ort und die zweite Gleichung partiel nach der Zeit abgeleitet. Eine Kombination der beiden Gleichungen f¨ uhrt zun¨ achst zur Wellengleichung f¨ ur den eindimensionalen Fall:

Im allgemeinen Fall gilt:

∆p − =

Die allgemeine L¨ osung ψ( r, t) der Wellengleichung kann sowohl f¨ ur eine skalare als auch f¨ ur eine vektorielle Gr¨ oße stehen.

Die Gleichung (8) beschreibt Transversal- und auch Longitudinalwellen. Es handelt sich um eine homogene, lineare Differentialgleichung. Das heißt, existieren zwei verschiedene L¨ osungen, so gilt nach dem Superpositionsprinzip, daß auch ihre Linearkombination eine L¨ osung der Differentialgleichung ist.

1.3.2 Interferenz von Wellen

Interferenz tritt auf, wenn sich mehrere Wellenz¨ uge unter bestimmten Bedingungen ¨ uberlagern. Das bedeutet, daß an manchen Orten des Raumes die Wellenz¨ uge sich ausl¨ oschen bzw. abschw¨ achen, an anderen Orten hingegen sich verst¨ arken, so daß Interferenzmuster entstehen. Diese Bedingungen sind:

Page 10

Ein besonderes lnterferenzerph¨ anomen entsteht, wenn sich zwei gleichfrequente Wellen gleicher Amplitude ¨ uberlagern, deren Ausbreitungsrichtungen genau

entgegengesetzt sind. Es kommt dann zur Bildung von stehenden Wellen. Dies passiert z.B. dann, wenn eine Welle an einer Grenzschicht reflektiert wird und sich mit der reflektierten Welle ¨ uberlagert.

Die mathematische Beschreibung stehender Wellen soll anhand ebener, harmonischer Wellen erfolgen.

Die einlaufende Welle besitzt die Form: y e = y 0 sin 2π

Die reflektierte Welle:

F¨ ur die entstehende ¨ Uberlagerung erh¨ alt man:

y(x, t) = y e (x, t) + y r (x, t) = 2y 0 cos

(Additionstheorem: sin α + sin β = 2 sin

2 Stehende Wellen im Hohlraum

2.1 Stehende Wellen im Quader

Zur Beschreibung der Schallwellen im Quaderhohlraum ziehen wir die Allgemeine Wellengleichung(10) heran.

∆Φ =

Da wir nur stehende Wellen betrachten wollen, bietet sich der Ansatz von Bernoulli (11) an. Danach wird die Φ-Funktion als als Produkt aus einem orts- und eines zeitabh¨ angigen Teil beschrieben.

Φ( r, t) = u( r) · v(t) (11)

Page 18

mit

f (t) = f 0 sin(ωt + α 1 ) ; ω = kc

g(φ) = g 0 sin(mφ + α 2 ) ; m ∈ Z

h(θ) = P l (cosθ)

R(r) = j l (kr)

2.2.1 Die Legendre-Polynome

Die Legndre-Polynome sind Bestandteil der L¨ osung des winkelabh¨ angigen Teils der Differentialgleichung:

Y (θ, φ) = h(θ)g(φ)

wobei

h(θ) = P l (cos θ) =

P l (cosθ) ist das Legendre-Polynom ersten Grades.

Eine grafische Darstellung der Legendre Polynome liefert die sog. Wolkendiagramme, die auch von den L¨ osungen der zeitunabh¨ angigen Schr¨ odinger-Gleichung her bekannt sind. Sie geben die Aufenthaltswahrscheinlichkeit des Elektrons in der Atomh¨ ulle in Abh¨ angigkeit von dem Winkel θ an. Zur Darstellung der Legendre-Polynome geht man wie folgt vor: Unter dem Winkel θ wird der Wert des Polynoms P l (cos θ) abgetragen. Hierbei gilt f¨ ur die positive z-Achse θ = 0.

Die Legendre-Polynome P l (cos θ)besitzen in ihrem Definitionsbereich π ≥ θ ≥ 0 genau l Nullstellen und sind rotationssymmetrisch zur z-Achse. Von daher beschreiben die Nullstellen der Polynome Knotenkegelfl¨ achen bei der Resonanz Schallwellen in der Hohlkugel.

F¨ ur ungerades l tritt als weitere Knotenkegelfl¨ ache die x-y Ebene auf.

2.2.2 Randbedingungen

Am Rand der Kugel (r = R) verschwindet die Radialkomponente der Schallschnelle

v r | r=R = 0

Wie bekannt, gilt:

Der Besselfunktionen j l (x) sind keine periodischen Funktionen, besitzen aber regelm¨ aßig wiederkehrende Maxima. Durch geeignete Wahl des Parameters k ist es

Page 19

m¨ oglich, die Funktion derart zu stauchen oder zu strecken, dass jedes beliebige Maximum gerade bei r = R zum Liegen kommt. Die L¨ osung h¨ angt von den zwei Quantenzahlen n,l ab und besitzt diskrete k-Werte.

k l,n =

Die folgende Tabelle enth¨ alt die Werte f¨ ur x l,n in Abh¨ angigkeit von n und l:

kc = ω = 2πν → ν =

Die Quantenzahl m besitzt keinen Einfluss auf die Frequenz. Die Rotationssymmetrie zur z-Achse f¨ uhrt zur m-Entartung. Im quantenmechanischen problem des Wasserstoffatoms liegt eine zweifache Entartung (m- und l-Entartung) vor.

2.3 Resonanz und Abklingdauer

In der Praxis zeigt es sich, dass die Resonanz in einem Hohlraum nicht diskret ist, sondern in einem Intervall um den Frequenzwert herum auftritt, dem Resonanzintervall. Dieses Resonanzintervall l¨ asst sich durch den Fourier-Ansatz, einer ¨ Uberlagerung ¨ uberabz¨ ahlbarer harmonischer Schwingungen, erkl¨ aren. Jede dieser Schwingungen besitzt ihre diskrete Resonanzfrequenz in diesem Intervall. Mit Hilfe einer Fourier-Transformation l¨ asst sich die Resonanzbreite ∆ν berechnen.

Page 21

Gesucht ist die Frequenz ω1 , bei der φ(ω) auf die H¨ alfte von φ(ω 0 ) abgesunken

2

ist:

φ(ω1

⇒

⇒

F¨ ur die D¨ ampfungskonstante δ gilt der Zusammenhang: τ = 1

δ

Daraus ergibt sich: ∆ν = 1

τ π

¨ Uber eine experimentelle Bestimmung der Abklingdauer l¨ asst sich somit die D¨ ampfungskonstante δ und die Resonanzbreite ∆ν bestimmen.

3 Der Wellencharakter von Teilchen

Der Physiker De Broglie stellte eine Beziehung auf, die dem Teilchen mit dem Impuls p eine Materiewell mit der Wellenl¨ ange λ zuordnet. Sie lautet λ = ^h .

p

In der Quantenmechanik wird ein Teilchen durch eine Wellenfunktion ψ( r, t) beschrieben, die alle Informationen (Impuls, Drehimpuls, Energie) ¨ uber das Teilchen enth¨ alt. Der Wellenfunktion selbst kommt keine anschauliche Funktion zu. Man erh¨ alt die Wellenfunktion ψ( r, t), indem man die Schr¨ odinger-Gleichung, eine partielle Differentialgleichung, l¨ ost. Die Schr¨ odinger-Gleichung(22) besitzt die Form:

−

Die nicht relativistische Schr¨ odinger-Gleichung gilt jedoch nur f¨ ur Fermionen, die sich in einem Potential V ( r) aufhalten.

In der Quantentheorie wird jeder klassischen Gr¨ oße, wie z.B. der Impuls und Energie, ein bestimmter Operator zugeordnet. So wird der Gesamtenergie E = E kin + E pot der Hamilton-Operator H = − h ² ∆ + V ( r) zugeordnet. Der Opera-

8π ² m

tor ist eine Rechenvorschrift, die auf die dahinterstehende Wellenfunktion ψ( r, t) wirkt. Um ein quantenmechanisches Problem zu l¨ osen, muss also die Schr¨ odinger-Gleichung gel¨ ost werden, in der f¨ ur V ( r) das problemspezifische Potential eingesetzt wird.

Im folgenden soll die Analogie des Problems eines Teilchens in einem dreidimensionalen Kastenpotential zum klassischen Fall einer stehende Schallwelle in einem Quderhohlraum aufgezeigt werden.

Page 23

Systems zu einem bestimmten Zeitpunkt (z.B. t = 0) bekannt sein muss, um durch eine Taylorentwicklung L¨ osungen f¨ ur alle Zeiten zu erhalten. Hingegen werden zur L¨ osung der Wellengleichung sowohl der Zustand des Systems zu einer bestimmten Zeit, als auch die erste zeitliche Ableitug zum Zeitpunkt t = 0 ben¨ otigt.

Die Schr¨ odinger-Gleichung ist im Gegensatz zur Wellengleichung komplex.

4 Das Wasserstoffatom

Auf das Wasserstoffatom wollen wir hier nur sehr kurz eingehen: Die zeitunabh¨ angige Schr¨ odinger-Gleichung(23):

Mit der reduzierten masse: µ = ^{me·m k} , wobei m e die Masse des Elektrons und

^me+m k

m k Masse des Kerns ist.

F¨ ur das Coulomb-Feld gilt: V (r) = − 1

Der Laplace-Operator in Polarkoordinaten: ∆ = 1

mit ψ(r, θ, φ) = R(r) · Θ(θ) · Φ(φ) folgt:

h 2 d

¯

sin θ

Die L¨ osungen der Radial- und der Polargleichung sind die sog. zugeordneten Laguerreschen-Polynome bzw. im zweiten Fall die uns bereits bekannten Legendreschen-Polynome.

5 Versuchsbeschreibung

5.1 Hohlraumresonanzen im Quader

5.1.1 Ziel des Versuchs

Es werden die Eigenschwingungen eines Quaders aufgenommen, die Eigenfrequqnzen gemessen und die Schwingungsmoden identifiziert. Ferner wird die Schallgeschwindigkeit unter Normalbedingungen berechnet. Desweiteren soll die Abklingdauer τ einer Resonanz und die Resonanzbreite ∆ν gemessen werden. Die Abmessungen des Quaders betragen L x = 0, 60965 m, L y = 0, 4253 m und L z = 0, 24135 m.

Page 24

5.1.2 Ermittlung der Schallgeschwindigkeit

Die Beschallung des Quaders geschieht durch einen Lautsprecher, der in einer Ecke des Hohlraums angebracht ist. Die Schwingungen werden durch einen Sinus-generator erzeugt. Zu Regelung der Frequenz wird ein Potentiometer eingesetzt, dessen abgegriffene Spannung an den x-Eingang des Schreibers gelegt ist. Die x- Achsestellt den Frequenzbereich ν dar, da die eingestellte Frequenz proportional zur angelegten Spannung ist. Die gemessene Schallintensit¨ at wird gleichgerichtet, uber eine Kondensator gegl¨ attet und auf den y-Eingang des Schreibers gelegt. Es ¨

wird der Frequenzbereich von 280 Hz bis 2000 Hz untersucht. Um eine h¨ ohere Aufl¨ osung zu erhalten, wird in zwei Durchg¨ ange unterteilt:

• 280 Hz bis 1200 Hz

• 1200 Hz bis 2000 Hz

Zur genauen Bestimmung der Resonanzfrequenzen wird Frequenzz¨ ahler verwendet (Vgl. Anhang ,,Versuchsaufbau”).

5.1.3 Messergebnisse und Auswertung

Die Aufzeichnug der Eigenschwingungen des Quaders befindet sich im Anhang. Zun¨ achst werden die gemessenen Frequenzen den berechneten zugeordnet. Zur Berechnung der theoretisch zu erwartenden Frequenzen ben¨ otigt man Schallgeschwindigkeit c, die man aus folgender Gleichung erh¨ alt:

ν =

Die Anwendung dieser Gleichung ist m¨ oglich, da dem Tripel (n x = 1 ; n y = 0 ; n z = 0) die tiefste Resonanzfrequenz (283, 2 Hz) zugeordnet werden muss.

Daraus ergibt sich f¨ ur die Schallgeschwindigkeit: c = 345, 306 m

s

Mit diesem Wert errechnen wir im folgenden die theoretisch zu erwartenden Werte der Resonanzfrequenzen und vergleichen sie mit den gemessenen. So kann man die Quantenzahlen(n x , n y und n z ) f¨ ur die gemessenen Frequenzen erhalten. Da die Berechnugen hierf¨ ur recht M¨ uhselig erscheinen, hat Herr Paulsen hierf¨ ur ein kleines Programm in der Programmiersprache ,,DIN 66256-Pascal ” geschrieben.

Page 27

Mittelwert aus 59 Werten: c = 345, 80 m

Der Fehler errechnet sich aus: ∆x =

F¨ ur die Schallgeschwindigkeit k¨ onnen wir also folgenden Wert angeben:

c = 345, 80 m s ± 0, 07 m

s

Da diese Messung bei 22, 1 ^◦ C durchgef¨ uhrt wurde, muss unser Ergebnis f¨ ur die Schallgeschwindigkeit auf die Temperatur 0 ^◦ C umgerechnet werden, um es mit

√

dem Literaturwert vergleichen zu k¨ onnen. Es gilt c =

tenexponent ist (κ Luf t = 1, 4), R die spezifische Gaskonstante (R Luf t = 287 J

und T die Temperatur in Kelvin. Womit folgt:

√

c(0 ^◦ C) = 345, 80

Nach der Fehlerfortpflanzung gilt f¨ ur den Umrechnungsfehler:

∆c(T 2 ) =

∆c(T 2 ) =

F¨ ur den Temperaturfehler ist es sicherlich angemessen, die Ablesegenauigkeit des Thermometers von ±0, 5 ^◦ C zu nehmen.

∆c(T 2 ) =

∆c(T 2 ) = 0, 31

Als Literaturwert findet man f¨ ur die Schallgeschwindigkeit bei 0 ^◦ C : c(0 ^◦ C) = 331, 45 m s . Mit unserem umgerechneten Wert von c(0 ^◦ C) = 332, 6 m s ± 0, 3 m

s weichen wir um 0, 4% vom Literaturwert ab. Da die Streuung der Werte f¨ ur die Schallgeschwindigkeit bei 22, 1 ^◦ C sehr gering ist, kann man vermuten, dass diese Abweichung systembedingt ist.

5.1.4 Resonanzbreite und Abklingdauer

In diesem Versuchsabschnitt soll die Beziehung zwischen Resonanzbreite ∆ν und der Abklingdauer τ best¨ atigt werden. Der erste Teil des Versuchsaufbaus stimmt

Page 28

mir dem des vorangegangenen Versuchs ¨ uberein. Der peak der niedrigsten Resonanzfrequenz 283, 8 Hz wird auf einen großen Bereich gestreckt, um an einigen Stellen der x-Achse abzutragen zwecks Bereitstellung eines Maßstabs. Auf halber H¨ ohe des Peaks wird seine Breite gemessen, die Resonanzbreite ∆ν. Im zweiten Teil des Versuchs wurde das Mikrofon an einen AD-Wandler gelegt, der die Amplituden registrierte. Nach Abstellen des Lautsprechers konnten die Amplitudenwerte des Abklingvorgangs vom Computer ausgegeben werden. (vgl. Anhang)

5.1.5 Messergebnisse und Auswertung

Als Resonanzbreite ergab sich(vgl Anhang): ∆ν = 4, 75 Hz

Im zweiten Versuchsteil gilt es die exponentiell abfallenden Amplitudenwerte A(t) auszuwerten. Da nur eine schwache D¨ ampfung angenommen wird, gilt:

A(t) = e ^−δt+b bzw. ln A(t) = −δt + b

Das Zeitintervall zwischen zwei Wertepaaren betr¨ agt ∆t = ¹ = ¹ s. Eine gra- ν 283,2

phische Darstellung von ln A(t) befindet sich im Anhang. Eine Lineare Regression f¨ ur Wertepaare, bei denen ln A(t) noch ann¨ ahernd einer geraden entspricht, ergibt:

δ = 14, 57

Durch die Lineare Regression erh¨ alt man mit der Gleichung ∆ν = ¹ = ^δ :

^{τ π π} ∆ν 2 = 4, 64 Hz

Es zeigt sich, dass die beiden Werte ∆ν 1 und ∆ν 2 um 2, 4% voneinander abweichen. Man muss hierbei aber ber¨ ucksichtigen, dass man durch die Wahl der Wertepaare f¨ ur die lineare Regression durchaus unterschiedliche Werte f¨ ur δ erhalten kann. Dennoch sind wir der ¨ Uberzeugung, dass unsere Auswahl der Wertepaare vertretbar ist.

5.2 Hohlraumresonanzen in der Hohlkugel

5.2.1 Ziel des Versuchs

In diesem Experiment soll die Schallgeschwindigkeit in Luft anhand von Hohlraumresonanzen in einer Hohlkugel bestimmt werden. Im zweiten Teil des Versuchs wird die radiale Verteilung des Schalldrucks mit einem mikrofon ausgemessen und mit der theoretisch zu erwartenden verglichen.

Page 29

5.2.2 Bestimmung der Schallgeschwindigkeit

Hierzu wird die hohlkugel (Radius R = 0, 14m mit einem Lautsprecher, der am Kugelrand diametral entgegengesetz zum Mikrofon angebracht ist, beschallt. Der Frequenzbereich liegt bei 800 bis 2900Hz. Mittels eines x-y-Schreibers werden die bei diskreten Frequenzen auftretenden Resonanzen aufgenommen. (s. Anhang)

5.2.3 Messergebnisse und Auswertung

Es gilt folgender Zusammenhang zwischen der Resonanzfrequenz ν l,n und der Schallgeschwindigkeit c in der Hohlkugel: x l,n · c

ν l,n =

Das weitere Vorgehen ist analog zu dem beim Quaderhohlraum. Zun¨ achst werden die Werte x l,n der Gr¨ oße nach sortiert, und dem kleinsten x l,n -Wert die nierigste von uns gemessene Resonanzfrequenz zugeordnet. Dies erm¨ oglicht die n¨ aherungsweise Berechnung der Schallgeschwindigkeit c. Mit diesem gen¨ ahertem Wert lassen sich nun die weiteren, theoretisch zu erwartenden Resonanzfrequenzen ¨ uber

die obige Beziehung berechnen und mit den gemessenen Frequenzen vergleichen.

Es ergibt sich folgende Schallgeschwindigkeit:

c = 353

Umgerechnet auf 0 ^◦ C:

c(0 ^◦ C) = 339, 91

Unter Ber¨ ucksichtigung der Fehlerfortplanzung (siehe Glg. 24):

c(0 ^◦ C) = 339

Wir weichen damit um 2, 55% vom Literaturwert von 331, 45 m

s ab.

Page 30

5.2.4 Messung der radialen Druckverteilung

in diesem Versuchsabschnitt soll wird mit dem Mikrofon die radiale Druckverteilung ausgemessen, graphisch ausgegeben und mit der theoretisch zu erwartenden Druckverteilung der Besselfunktion verglichen.

Der Versuchsaufbau ist identisch mit dem im vorangegangenen Abschnitt. Die Frequenz ν = 2901, 2Hz wird eingestellt und w¨ ahrend der Durchf¨ uhrung konstant gehalten. Der x-Eingang des Schreibers wird gel¨ ost und per Hand ¨ uber

die Einstellschraube bedient. Anschließend wird das Mikrofon in Intervallen der Breite von 0, 5cm in die Kugel hinein gef¨ uhrt. Gleichzeitig wird die x-Position des Schreibers ebenfalls um einen halben Zentimeter nach rechts verschoben. In gleichen Abst¨ anden wird so der Schalldruck innerhalb der Hohlkugel gemessen und in Abh¨ angigkeit vom Radius graphisch dargestell (vgl Anhang).

5.2.5 Messergebnisse und Auswertung

Die Frequenz ν = 2901, 2Hz, bei der die radiale Druckverteilung gemessen wird, l¨ asst sich den Quantenzahlen l = 2 und n = 2 zuordnen. Dies entspricht einer theoretisch zu erwartenden Frequenz von ν = 2925, 4Hz, wenn man die soeben bestimmte Schallgeschwindigkeit annimmt. Es ergibt sich:

j 2 (k 2,2 · r) =

und k 2,2 =

Page 34

B Quaderesonanzen

Von 280 bis 1420Hz:

Von 1420 bis 2408Hz:

Page 35

C Abklingdauer

Amplituden in Abh¨ angigkeit von der Zeit:

Logarithmus der Amplituden (ln A(t)) in Abh¨ angigkeit von der Zeit:

Page 37

D Resonanzen der Hohlkugel

Resonanzen von 799 bis 2254Hz:

Resonanzen von 1340 bis 2408, 3Hz:

Page 38

E Radiale Druckverteilung in der Hohlkugel

Gemessene radiale Druckverteilung in der Hohlkugel:

Druckverteilung in der Hohlkugel (Vergleich Theorie und Messwerte):