Allgemeine Schaltkreise II

Page 1

Page 2

Allgemeine Schaltkreise II Einleitung

Einleitung

Ein Boolescher Schaltkreis S (im folgenden nur Schaltkreis genannt) ist ein gerichteter azyklischer Graph. Die Knoten von S mit dem Eingangsgrad (engl. fan-in) 0 sind die Eingaben (Variablen oder die Konstanten 0 und 1). Die Knoten von S mit einem Eingangsgrad k > 0 sind die Gatter. Sie repräsentieren eine Boolesche Funktion mit k Eingaben. Einer der Knoten von S liefert die Ausgabe des Schaltkreises. Als n(S) bezeichnet man die Anzahl der verschiedenen Variablen des Schaltkreises S. Die Größe (oder Komplexität) von S, C(S), ist die Anzahl der Gatter von S. Die Tiefe von S, D(S), ist die maximale Länge eines Pfades von der Eingabe zur Ausgabe.

Ein Schaltkreis S repräsentiert auf natürliche Weise eine Boolesche Funktion

{ } { } ⁼ → n ) S ( n . 1 , 0 1 , 0 : f

Die Menge aller Booleschen Funktionen mit n Variablen bezeichnet man als B n . Für Boolesche

Funktionen f ∈ B n existieren 2 ⁿ verschiedene Eingaben, wobei jede dieser Eingaben entweder auf

0 oder auf 1 abgebildet werden kann. Es gilt daher die folgende Gleichung:

B = n 2 2

n

Um Aussagen über die Komplexität einer beliebigen Booleschen Funktion f machen zu können, definiert man C(f) als die Größe des kleinsten Schaltkreises, der f berechnet, d.h.

{ } C = f berechnet S : C(S) min ) f (

Die Komplexität einer Klasse von Booleschen Funktionen ist gleich der Komplexität der härtesten Booleschen Funktion in dieser Klasse. Z.B. gilt für die Komplexität der Klasse der Booleschen Funktionen mit n Variablen

{ } ∈ = B f : ) f ( C max ) B ( C

n n

Das Ziel dieses Seminarvortrages ist es, für beliebige Boolesche Funktionen f mit n Variablen asymptotische Aussagen über die Größe des kleinsten Schaltkreises, der f berechnet, zu machen. Dabei werden allgemeine Schaltkreise, also Schaltkreise ohne Einschränkungen bezüglich der Größe und Tiefe betrachtet. Wenn nichts anderes erwähnt wird, betrachten wir im folgenden B 2 -Schaltkreise, d.h. wir betrachten Schaltkreise, deren Gatter einen fan-in von kleiner gleich 2 haben und alle Booleschen Funktionen aus B 2 berechnen können.

Asymptotische Aussagen

Sei f: N → N eine Funktion. Dann bezeichnen O(f), Ω(f) und o(f) folgende Mengen von

Funktionen:

{ }

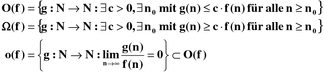
Wir benutzen die O- bzw. die o-Notation in Beweisen von oberen Schranken und die Ω-Notation

in Beweisen von unteren Schranken.

Page 3

Allgemeine Schaltkreise II Der Shannon-Effekt

Der Shannon-Effekt

1. Formulierung:

Nahezu alle Booleschen Funktionen mit n Variablen besitzen näherungsweise die gleiche Komplexität wie die härteste Boolesche Funktion mit n Variablen. 2. Formulierung:

Für nahezu alle Booleschen Funktionen mit n Variablen besitzen optimale Schaltkreise eine exponentielle Größe bei linearer Tiefe.

Die zweite Formulierung ist der ersten vorzuziehen, da in ihr explizit eine Größen- bzw. Tiefenaussage über optimale Schaltkreise gemacht wird.

Bevor wir den Shannon-Effekt für die Klasse der Booleschen Funktionen mit n Variablen und B 2 -Schaltkreise beweisen, verdeutlichen wir uns die Aussage durch ein Abzählargument: Einerseits gibt es nicht sehr viele Schaltkreise mit geringer Größe, andererseits existieren sehr viele Boolesche Funktionen mit n Variablen.

Definition

Die bereits des öfteren benutzte Redewendung "nahezu alle Booleschen Funktionen f besitzen die Eigenschaft e" bedeutet mathematisch ausgedrückt:

{ }

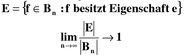
Andere Formulierung: Wenn wir n nur genügend groß wählen, dann besitzen vernachlässigbar wenige Funktionen f die Eigenschaft e nicht.

Page 4

Allgemeine Schaltkreise II eine untere Schranke für nicht-explizite Probleme

eine untere Schranke für nicht-explizite Probleme

Obwohl wir meistens mit explizit angegebenen Problemen (z.B. die Probleme in P oder NP) arbeiten, ist es auch sehr wichtig zu wissen, welche Aussagen man über nicht-explizite Probleme machen kann. Dazu betrachten wir das folgende Theorem (in Anlehnung an: [1], Theorem 2.4.):

Nahezu jede Boolesche Funktion mit n Variablen benötigt Schaltkreise der Größe Ω(2 n /n).

Beweis:

Zuerst zeigen wir, daß die Anzahl der Schaltkreise mit n Variablen und der Größe s nach oben beschränkt ist durch

{ } + + ⋅ ≤ = = . s 2 ) ) 2 n s ( 16 ( s ) S ( C , n ) S ( n : S

Jedes Gatter in einem Schaltkreis berechnet eine von |B 2 | = 16 Funktionen mit 2 Eingaben. Jede

dieser Eingaben kann entweder ein vorhergehendes Gatter (höchstens s Möglichkeiten), eine Variable (n Möglichkeiten), oder eine Konstante (2 Möglichkeiten) sein. Demnach haben wir pro Gatter höchstens 16⋅(s+n+2) ² Möglichkeiten. Faßt man diese Möglichkeiten für alle s Gatter zusammen, so ergibt sich die obere Schranke.

Um zu der Aussage des Theorems zu gelangen, müssen wir s geeignet wählen und dann zeigen, daß nur sehr wenige Boolesche Funktionen mit Schaltkreisen der Größe s berechnet werden können. Wir wählen s = 2 ⁿ /(10n):

Für s = 2 ⁿ /(10n) ist die obere Schranke für die Anzahl der Schaltkreise näherungsweise (siehe mathematischer Anhang) 2 ^{2 n /5} << 2 ^{2 n} . Da aber 2 ^{2 n} Boolesche Funktionen mit n Variablen

existieren und jede dieser Booleschen Funktionen durch einen anderen Schaltkreis berechnet wird, benötigt nahezu jede Boolesche Funktion mit n Variablen Schaltkreise mit einer Größe von mehr als 2 ⁿ /(10n) Gatter. Damit ist das Theorem bewiesen.

Eine weitere untere Schranke für nicht-explizite Probleme

Im folgenden schätzen wir die Anzahl der verschiedenen Schaltkreise der Größe s ab. Es gilt das Lemma ([2], Lemma 4.2.1.): Höchstens

⋅ + + ⋅ = s 2 s ! s / s ) 1 n s ( 16 ) n , s ( S

Boolesche Funktionen f ∈ B n können durch B 2 -Schaltkreise der Größe s berechnet werden.

Beweis:

Jedes einzelne der s Gatter kann eine der |B 2 | = 16 verschiedenen Booleschen Funktionen mit

2 Eingaben berechnen. An jedem der s Gatter gibt es s+n+1 Möglichkeiten der Wahl jedes Eingangs (die anderen s-1 Gatter, n Variablen und 2 Konstanten). Wir können unter allen Ausgaben der s Gatter eine Ausgabe als Gesamtausgabe des Schaltkreises wählen. Zuletzt müssen wir noch berücksichtigen, daß bei unserer Zählung jeder Schaltkreis s!-mal gezählt

Page 5

Allgemeine Schaltkreise II eine weitere untere Schranke für nicht-explizite Probleme

wurde (die s! verschiedenen Möglichkeiten der Numerierung der einzelnen Gatter). Insgesamt erhalten wir die oben behauptete Schranke. Theorem ([2], Theorem 4.2.1.):

Für genügend große n haben mindestens |B n |⋅(1-2 -r(n) ), mit r(n) = 2 n /n⋅log 2 log 2 n, der |B n | Booleschen Funktionen in B n eine Schaltkreisgröße von mindestens 2 n /n. Vor allem haben nahezu alle Booleschen Funktionen f ∈ B n eine Schaltkreisgröße von mindestens 2 n /n.

Beweis:

Wenn wir s = s(n) = C(B n ) setzen, dann können mindestens alle |B n | Booleschen Funktionen aus B n durch einen Schaltkreis der Größe s berechnet werden. Mit Hilfe des gerade bewiesenen Lemmas können wir schließen:

Durch Einsetzen der Stirlingschen Näherungsformel

^{− +} ⋅ ⋅ ≥ s 2 / 1 s e s c ! s

für eine Konstante c > 0 erhalten wir nach Logarithmieren

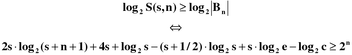
Für ein genügend großes n gilt s ≥ n+1 und deshalb

≥ − ⋅ + ⋅ + + ⋅ n 2 c log s log 2 / 1 s ) e log 6 ( s log s

2 2 2 2

Für s ≤ 2 ⁿ /n schließen wir

was für genügend große n falsch ist. Deshalb gilt für genügend große n

n ≥ = n n / 2 ) B ( C s

Wir können noch mehr beweisen. Wenn wir eine Untermenge B n

^* ) ≥ 2 ⁿ /n für genügend große n. Gewöhnlich
können wir in der gleichen Weise zeigen, daß C(B ⁿ wählen wir B

ⁿ Schaltkreisgrößen. Wenn wir für diese Menge die untere Schranke gezeigt haben, dann besitzen zwangsläufig alle anderen Booleschen Funktionen in B n noch größere Schaltkreise. Damit ist das Theorem bewiesen.

Page 6

Allgemeine Schaltkreise II eine obere Schranke

Eine obere Schranke

Eine triviale obere Schranke ist n⋅2 ⁿ +n-1. Beweis: Man kann jede Boolesche Funktion f ∈ B n

in der disjunktiven Normalform (DNF), d.h. als Disjunktion ihrer Minterme, darstellen. Es existieren maximal 2 ⁿ verschiedene Minterme, für deren Berechnung wir jeweils genau n-1 UND-Gatter benötigen, wenn wir die Negationen der n Variablen schon vorliegen haben. Es folgt

C(B n ) ≤ (n-1 UND-Gatter)⋅2 n +(2 n -1 ODER-Gatter)+(n NICHT-Gatter) = n⋅2 n +n-1 Gatter

Wir werden im folgenden eine sehr viel bessere obere Schranke beweisen: Theorem ([2], Theorem 4.2.2.):

Es gilt für alle f ∈ B n + ≤ n n ) n / 2 ( o n / 2 ) f ( C

Beweis:

Wir betrachten im folgenden 3 verschiedene Beweisansätze, von denen aber letztlich nur der dritte Ansatz das geforderte Resultat liefern wird. 1. Ansatz:

Wir betrachten dazu eine bekannte Darstellung einer beliebigen Booleschen Funktion f, die

∈ B n-1 die Booleschen Unterfunktionen von f ∈ B n für ^{(i) (i)} Shannon'sche Entwicklung: Seien f 0 , f 1

x i = 0 und x i = 1. Es gilt dann die Darstellung

∧ ∨ ∧ = ) i ( ) i ( ) f x ( ) f x ( f

1 i 0 i

∈ B n-1 kann die Shannon'sche Entwicklung weiter fortgesetzt ^{(i) (i)} Für die Unterfunktionen f 0 , f 1

werden. Graphisch kann man sich die ersten beiden Shannon'schen Entwicklungsschritte der

Booleschen Funktion f als vollständigen binären Baum der Tiefe 2 vorstellen (mit i ≠ j):

Die Boolesche Funktion f ∈ B n besitzt 2 Boolesche Unterfunktionen aus B n-1 , 4 Boolesche Unterfunktionen aus B n-2 , oder allgemein ausgedrückt 2 ^n-k Boolesche Unterfunktionen aus B k .

Eine direkte Umsetzung von f in einen sogenannten dekodierten Schaltkreis (engl. decoding circuit) liefert keine effiziente Lösung. Es gilt nämlich die Rekursionsungleichung

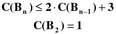
mit der Lösung

− ≤ n 3 2 ) B ( C

n

Dekodierte Schaltkreise sind nur eine theoretische Beschreibungsmöglichkeit. Man kann sie leicht verbessern, wie wir im nun folgenden 2. Ansatz sehen werden.

Page 7

Allgemeine Schaltkreise II eine obere Schranke

2. Ansatz:

In diesem Ansatz verwenden wir folgende Ideen:

• Wir berechnen alle 2 ^n-k Booleschen Unterfunktionen von f in B k im voraus in unabhängigen Teilschaltkreisen

• Danach führen wir die Shannon'sche Entwicklung bis zur Rekursionstiefe n-k durch

Sei nun C ^* (B k ) die Schaltkreiskomplexität für die Berechnung aller Booleschen Funktionen in B k . Es gilt analog zur Shannon'schen Entwicklung

mit der Lösung

^{− ∗} ⋅ + ⋅ ≤ 1 k k 2 2 2 6 2 3 ) B ( C

k

Wir benötigen noch das folgende Lemma:

Es sind 3⋅2 n-k -3 Gatter zur Berechnung von f ausreichend, wenn die Booleschen Funktionen in B k gegeben sind. Beweis:

Wir betrachten hierfür noch einmal die ersten beiden Entwicklungsschritte der Shannon'schen

Entwicklung von f und den dazugehörenden Entwicklungsbaum (mit i ≠ j):

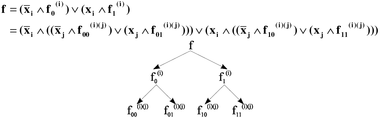
Ein Entwicklungsbaum der Tiefe t besitzt 2 ^t -1 innere Knoten. Pro inneren Knoten benötigt man 3 Gatter (siehe Formel). Setzen wir t = n-k, dann folgt das Lemma.

Es folgt (für beliebiges k)

^{− − −} ⋅ + + ⋅ ≤ + − ⋅ = 1 k k 2 2 k n * k n 2 6 ) 2 2 ( 3 ) B ( C 3 2 3 ) B ( C

k n

Setzt man k = log 2 n-1, dann folgt (siehe mathematischer Anhang) + ⋅ ≤ n n ) n / 2 ( o n / 2 12 ) B ( C

n

Diese einfachen Ideen haben uns zu Schaltkreisen geführt, deren Größen nur um den Faktor 12 höher liegen als die Größe eines optimalen Schaltkreises. Um aber den Faktor 12 eliminieren zu können, muß man einen anderen Ansatz wählen, der um einiges komplizierter sein wird.

Page 8

Allgemeine Schaltkreise II eine obere Schranke

3. Ansatz:

Im folgenden betrachten wir die sogenannte (k,s)-Lupanov-Darstellung für Boolesche

Funktionen. Wir stellen die Funktionswerte von f ∈ B n in einer 2 ^k × 2 ^n-k -Matrix dar.

Dabei stehen jede der 2 ^k Zeilen für genau einen der 2 ^k verschiedenen Werte von (x 1 ,..., x k ) und jede der 2 ^n-k Spalten für genau einen der 2 ^n-k verschiedenen Werte von (x k+1 ,..., x n ). An der Matrixposition x ij (1 ≤ i ≤ 2 ^k , 1≤ j ≤ 2 ^n-k ) steht genau dann eine 1 (bzw. 0), wenn die

Funktion f auf die von der i-ten Zeile und der j-Spalte repräsentierten Eingabe eine 1 (bzw. 0) liefert.

Die Zeilen sind in p = 2 ^k /s ≤ 2 ^k /s+1 Blöcke A 1 ,..., A p unterteilt, so daß A 1 ,..., A p-1 s Zeilen und A p s' ≤ s Zeilen enthält.

Wir versuchen nun, einfachere Boolesche Funktionen als f zu finden und f auf einige von diesen einfacheren Booleschen Funktionen zu reduzieren:

• Sei

Offensichtlich gilt dann

• Sei (für i < p ist w ∈ {0,1} ^s , für i = p ist w ∈ {0,1} ^s' )

B i,w = Menge der Spalten, deren Schnittpunkte mit A i gleich w ist

• Sei

Dann gilt

∨ = ) x ( f ) x ( f

w , i i w

• Wir betrachten nun die 2 ^k ×2 ^n-k -Matrix von f i,w . Alle Zeilen außerhalb von A i bestehen nur aus

Nullen, die Zeilen von A i haben nur zwei verschiedene Typen von Spalten: w oder Spalten nur

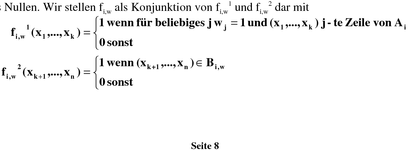
aus Nullen. Wir stellen f i,w als Konjunktion von f i,w

Page 9

Allgemeine Schaltkreise II eine obere Schranke

Insgesamt erhalten wir die (k,s)-Lupanov-Darstellung

Wir berechnen f auf folgende Weise:

Schritt 1:

Wir berechnen mit O(2 k +2 n-k ) Gatter alle Minterme von (x 1 ,...,x k ) und von (x k+1 ,..., x n ). Schritt 2:

¹ mit deren DNF. Die Minterme sind schon berechnet. Weil die Blöcke Wir berechnen alle f i,w

A i alle unabhängig voneinander sind, wird jeder Minterm höchstens einmal für ein festes w

benötigt. Insgesamt sind daher 2 s ⋅2 k Gatter nötig.

Schritt 3:

² mit deren DNF. Die Minterme sind schon berechnet. Weil die Blöcke Wir berechnen alle f i,w

B i,w für ein festes i alle unabhängig voneinander sind, wird jeder Minterm höchstens einmal für ein festes i benötigt. Insgesamt sind p⋅2 n-k Gatter nötig. Schritt 4:

Es sind 2p⋅2 s Gatter ausreichend, um f zu berechnen, wenn alle f ^{i,w 1} und f ^{i,w 2} vorliegen.

Die Anzahl der Gatter unseres Schaltkreises kann wegen p ≤ 2 ^k /s+1 abgeschätzt werden mit ^{+ + + − + −} + + + + + + 1 s 1 s k k n n k s k n k 2 s / 2 2 s / 2 2 ) 2 2 ( O

Wählt man k = 3⋅log 2 n und s = n-5⋅log 2 n, dann erhält man die Aussage des Theorems

(siehe mathematischer Anhang).

Eine kurze Zusammenfassung

Bis jetzt haben wir gezeigt, daß (nahezu) alle Booleschen Funktionen mit n Variablen durch Schaltkreise mit mindestens 2 ⁿ /n und höchstens 2 ⁿ /n+o(2 ⁿ /n) Gatter berechnet werden können. Für große n kann man o(2 ⁿ /n) in diesem Zusammenhang vernachlässigen. Dann folgt, daß (nahezu) alle Booleschen Funktionen mit n Variablen die gleiche (exponentielle) Schaltkreiskomplexität bei linearer Tiefe besitzen. Damit haben wir bewiesen, daß der Shannon-Effekt für B n und B 2 -Schaltkreise gültig ist.

Page 10

Allgemeine Schaltkreise II eine untere Schranke für ein explizites Problem

eine untere Schranke für ein explizites Problem

Trotz der Wichtigkeit der unteren Schranken expliziter Probleme in der Schaltkreiskomplexität sind die besten bis jetzt bekannten unteren Schranken nur linear. Die Beweise dieser unteren Schranken benutzen die im folgenden erklärte Gatter-Eliminationsmethode:

Ist für eine gefragte Boolesche Funktion ein Schaltkreis gegeben, so wird im allgemeinen eine Variable (oder eine Menge von Variablen) mit mehreren Gattern verbunden sein. Setzt man nun diese Variable auf einen konstanten Wert, so werden einige Gatter überflüssig und eliminiert. Bei wiederholter Anwendung dieser Methode können wir schließen, daß der ursprüngliche Schaltkreis sehr viele Gatter besaß.

Als Beispiel werden wir die Gatter-Eliminationsmethode an Schwellen-Funktionen (engl. threshold functions) anwenden. Eine Schwellen-Funktion TH k,n ist folgendermaßen definiert:

{ } { }

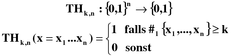
Wir betrachten zur besseren Verständlichkeit des nun folgenden Theorems die vollständige

Basis B = {∧, ∨, ¬}. Das Theorem verliert seine Gültigkeit aber auch dann nicht, wenn wir als

Basis B 2 wählen. Es gilt das Theorem ([1], Theorem 2.5.):

Für n ≥ 2 benötigt die Boolesche Funktion TH 2,n einen Schaltkreis mit einer Mindestgröße von

2n-4.

Beweis:

Wir beweisen diese Behauptung durch Induktion nach n. Für n = 2 und n = 3 ist die Schranke trivial. Angenommen, wir besitzen bereits einen optimalen Schaltkreis S o für die Boolesche Funktion TH 2,n . Ohne Beschränkung der Allgemeinheit nehmen wir an, daß das erste Gatter von

S o die Variablen x i und x j (mit i ≠ j) miteinander verknüpft:

Unter den vier möglichen Wertekombinationen von x i und x j besitzt die Boolesche Funktion TH 2,n drei mögliche Boolesche Unterfunktionen:

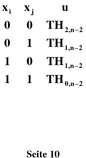
Page 11

Allgemeine Schaltkreise II eine untere Schranke für ein explizites Problem

Es folgt, daß entweder x i oder x j mit einem anderen Gatter von S o verbunden ist. Andernfalls hätte der Schaltkreis S o nur zwei nichtäquivalente Unterfunktionen unter der Wertebelegung von x i und x j , da nur noch die Ausgabe von g für den restlichen Schaltkreis verfügbar ist.

Wir nehmen nun an, daß die Variable x i mit einem anderen Gatter verbunden ist:

Setzen wir x i auf 0, dann eliminieren wir dadurch die Notwendigkeit für mindestens zwei Gatter (g und g') von S o , da wir das Ergebnis von g und g' ohne Kenntnis von x j und e berechnen können:

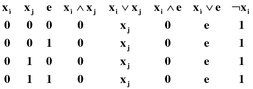
Die daraus resultierende Boolesche Funktion ist TH 2,n-1 , welche nach der Induktionsvorraussetzung einen Schaltkreis mit einer Mindestgröße von 2(n-1)-4 benötigt. Addiert man die zwei eliminierten Gatter zu diesem Wert hinzu, dann zeigt dies, daß S ^o mindestens 2n-4 Gatter benötigt. Damit ist der Induktionsbeweis abgeschlossen.

Bemerkung: Wir haben zwar gezeigt, daß jeder Schaltkreis, der die Funktion TH 2,n berechnet, mindestens 2n-4 Gatter benötigt, aber wir haben keinen Hinweis für die Konstruktion eines optimalen Schaltkreises für TH 2,n oder auf die tatsächliche Größe dieses Schaltkreises erhalten.

Page 12

Allgemeine Schaltkreise II Literaturliste

Literaturliste

[1] R. Boppana and M. Sipser, The Complexity of Finite Functions, in: Handbook of Theoretical Computer Science, (J. van Leeuwen, ed.), Elsevier, Amsterdam, The Netherlands, 1990, pp. 757-804.

[2] I. Wegener, The Complexity of Boolean Functions, Teubner, Stuttgart, Germany, 1987.

Page 13

Allgemeine Schaltkreise II Mathematischer Anhang

In die Formel

+ + ⋅ s 2 ) ) 2 n s ( 16 (

setzen wir s = 2 ⁿ /(10n) ein. Es gilt dann die Abschätzung < + + ⋅ n 5 / 2 s 2 2 ) ) 2 n s ( 16 ( Beweis:

In die Formel

setzen wir k = log 2 n -1 ein. Daraus folgt dann

+ ⋅ ≤ n n ) n / 2 ( o n / 2 12 ) B ( C

n

Beweis:

Es gilt log 2 n -2 < k ≤ log 2 n -1 Fall 1: n ist eine Zweierpotenz ⇒ k = log 2 n -1

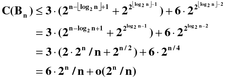
Fall 2: n ist keine Zweierpotenz

worst case: n+1 ist eine Zweierpotenz, für große n gilt k → log 2 n -2

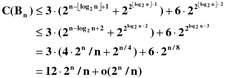
Insgesamt gilt die obere Schranke.

Page 14

Allgemeine Schaltkreise II Mathematischer Anhang

In die Formel

^{+ + + − + −} + + + + + + ≤ 1 s 1 s k k n n k s k n k 2 s / 2 2 s / 2 2 ) 2 2 ( O ) B ( C

n

setzen wir k = 3⋅log 2 n und s = n- 5⋅log 2 n ein. Es gilt dann + ≤ n n ) n / 2 ( o n / 2 ) B ( C

n

Beweis:

Es gilt 3⋅log 2 n ≤ k < 3⋅log 2 n +1, n-5⋅log 2 n -1 < s ≤ n-5⋅log 2 n Fall 1: n ist eine Zweierpotenz ⇒ k = 3⋅log 2 n, s = n-5⋅log 2 n

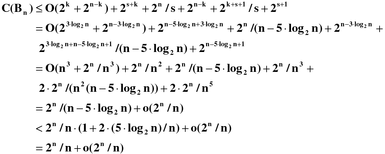
Fall 2: n ist keine Zweierpotenz ⇒ k → 3⋅log 2 n +1, s → n-5⋅log 2 n -1

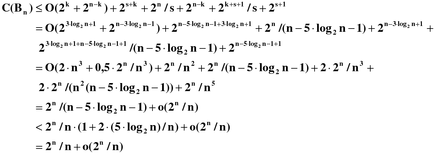
Insgesamt gilt die obere Schranke.