Elliptische Kurven - Elementare Theorie derselben

Page 1

Page 2

Elementare Theorie Elliptischer Kurven

1. Einleitung

Die vorliegende Ausarbeitung über Elliptische Kurven ist im Rahmen meines Vortrags  im Proseminar Elementare Zahlentheorie und Kryptologie enstanden. Ihr Ziel ist es,  einen ersten, kurzen Einblick in die Theorie Elliptischer Kurven zu geben. Dabei wird  der Verdeutlichung der wesentlichen Eigenschaften und Fragestellungen der Vorzug  vor   einer   möglichst   ausführlichen,   in   die   Tiefe   gehenden   Darstellung   der   Theorie  gegeben. Zu diesem Zweck sind zahlreiche Beispiele enthalten.

Zunächst  wird  der  Begriff  der  Elliptischen Kurve  bestimmt  und  im  Anschluss  eine  Addition auf ihr erklärt, welche diese Kurven zu einer abelschen Gruppe macht. Das Kapitel 4 widmet sich schließlich Elliptischen Kurven  über endlichen Körpern,  insbesondere ihrer Elementezahl und Gruppenstruktur.

2.Begriffsbestimmung

Definition 1a) Sei  K ein Körper mit char K ≠2,3 ,  x ³ axb mit  a , b ∈ K ein Polynom 3. Grades ohne vielfache Nullstellen. Dann heißt die Menge

{ x , y  ∈ K ×K ∣ y ² =x ³ axb } ∪ {0}   (1)

elliptische Kurve über  K . 

Dabei   heißt O Punkt   im   Unendlichen,   auf   seine   Bedeutung   wird   in   Kapitel   3  eingegangen.

Erinnerung Ein normiertes Polynom besitzt genau dann vielfache Nullstellen, wenn  seine Diskrimante Null ist. Die Diskriminate eines Polynoms der Form  x ³ axb ist gleich  4a ³ 27b ² .

Definition 1b) Sei  K ein Körper mit char K =2 , x ³ axb mit  a , b ∈ K ein  Polynom 3. Grades. Dann heißt

{ x , y  ∈ K ×K ∣ y ² y=x ³ axb } ∪ {0}   (2)

elliptische Kurve über  K .

Seite 2 von 12

Page 3

Elementare Theorie Elliptischer Kurven

Definition   1c)  Sei   K ein   Körper   mit char K =3 , x

Dann heißt

{ x , y  ∈ K ×K ∣ y ² =x ³ ax ² bxc } ∪ {0}   (3)

elliptische Kurve über  K .

Beispiel   1  { x , y  ∈ ℝ×ℝ ∣ y ³ −x } ∪ {0 } ist   eine   Elliptische   Kurve   über  ² =x

dem   Körper   der   reellen   Zahlen   (welcher   ja   Charakteristik   0   besitzt),   da   die  Diskrimante   des   Polynoms   auf   der   rechten   Seite   der   Gleichung 4⋅−1 ³ 27⋅0 ² =−4≠0 ist und damit dieses Polynom keine vielfachen Nullstellen  besitzt.

Der Graph dieser Elliptischen Kurve sieht über  [−2,2 ]×[−2,2 ] wie folgt aus:

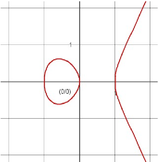
Man sieht sofort, dass die Kurve symmetrisch zur x­Achse ist.

3.Addition auf Elliptischen Kurven

Als   motivierendes   und   anschauliches   Beispiel   soll   uns   zunächst   die   Addition   auf  Elliptischen Kurven über den reellen Zahlen dienen. In diesem Kapitel sei  E eine durch  y ³  ax  b definierte Elliptische Kurve  ² = x über ℝ .

Definition   2  Sei   P =  x 1, y 1  ∈ E ∖ {0} .   Dann   definieren   wir −P   als 

Seite 3 von 12

Page 4

Elementare Theorie Elliptischer Kurven

Bemerkung 1  Da für   x , y ∈ ℝ aus   y

folgt, folgt aus  P ∈ E −P ∈ E .

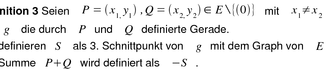
Definition 3 Seien  P =  x 1, y 1  , Q =  x 2, y 2  ∈ E ∖ {0} mit  x 1 ≠x 2 . Sei g  die durch  P und  Q definierte Gerade. Wir definieren S  als 3. Schnittpunkt von  g mit dem Graph von  E . Die Summe PQ wird definiert als  −S . Als Veranschaulichung dient uns  Beispiel 2

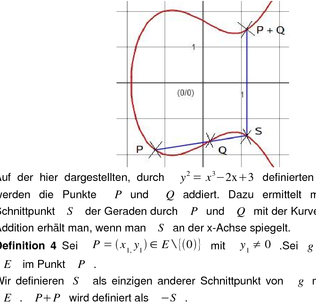
Auf   der   hier   dargestellten,   durch   y ² = x ³ −2x3 definierten   Elliptischen   Kurve  werden   die   Punkte   P und   Q addiert.   Dazu   ermittelt   man   zunächst   den  Schnittpunkt  S  der Geraden durch  P und  Q mit der Kurve. Das Ergebnis der  Addition erhält man, wenn man  S an der x­Achse spiegelt.

Definition  4  Sei   P =  x 1, y 1  ∈ E ∖ {0} mit   y 1 ≠ 0 .Sei g   die  Tangente  an 

Wir definieren S   als einzigen anderer Schnittpunkt von   g mit dem Graph von 

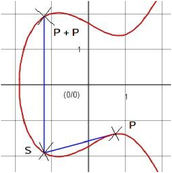
Als Illustration dieses Falls dient uns Beispiel 3 

Seite 4 von 12

Page 5

Elementare Theorie Elliptischer Kurven

Hier   wird   auf   derselben   Kurven   wie   in   Beispiel   2   der   Punkt   P zu   sich   selbst  addiert. Dazu ermittelt man die Tangente an der elliptischen Kurve in diesem Punkt.  Es   existiert   genau   ein   weiterer   Schnittpunkt   S dieser   Tangente   mit   der   Kurve. 

PP erhält man schließlich, wenn man  S an der x­Achse spiegelt.

Definition   5  Seien   P , Q ∈ E ∖ {0} mit   Q=−P .   PQ wird   definiert   als 

P0  definieren wir genauso wie   0  P als   P und schließlich setzen wir 

Bemerkung 2  Im Fall   Q = −P schneidet die Gerade durch   P und   Q , die  parallel zur y­Achse verläuft, den Graphen der Kurve in keinem weiteren Punkt. Nun  stellt man sich vor, dass diese Gerade einen Punkt, der sich „unendlich weit oben“  befindet, trifft. Dieser Punkt ist der Punkt im Unendlichen,  0 .

Wir haben noch zu zeigen, dass der Schnittpunkt  S aus Definition 3 und Definition  4 tatsächlich existiert und eindeutig bestimmt ist. Die geschieht in  Satz 1

a) Seien   P ,Q , g wie   in   Definition   3.   Dann   existiert   genau   ein   weiterer 

Schnittpunkt

b) Seien   P , g wie   in   Definition   4.   Dann   existiert   genau   ein   weiterer  Schnittpunkt

Beweis

zu  a)   g wird  durch  die   Gleichung y= x dargestellt,   da   g aufgrund   von 

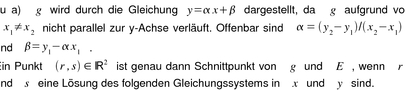
und  = y 1 − x 1 . 

Ein Punkt  r , s ∈ ℝ ² ist genau dann Schnittpunkt von  g und  E , wenn  r und  s eine Lösung des folgenden Gleichungssystems in  x und  y sind.

Seite 5 von 12

Page 6

Elementare Theorie Elliptischer Kurven

Dessen Lösungen erhalten wir, indem wir (4) in (5) einsetzen, wir erhalten:

und formen um zu x ³ − ² x ²  a−2   xb− ² = 0 .

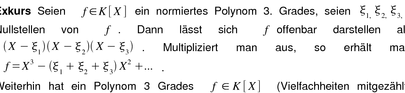
Exkurs  Seien   f ∈ K [ X ] ein   normiertes   Polynom   3.   Grades,   seien  1,  2,  ^3, Nullstellen   von   f .   Dann   lässt   sich   f offenbar   darstellen   als 

Weiterhin   hat   ein   Polynom   3   Grades   f ∈ K [ X ]   (Vielfachheiten   mitgezählt)  entweder 0, 1 oder 3 Nullstellen.

Wir wissen: Die x­Koordinaten x 1 und  x 2 von  P und  Q sind Nullstellen, weil  diese Punkte sowohl auf der Kurve als auch auf der Geraden liegen. Also ergibt sich gemäß unserem Exkurs:

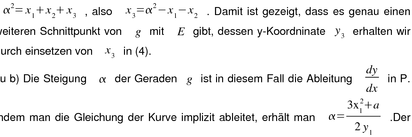
weiteren Schnittpunkt von  g mit  E gibt, dessen y­Koordninate y 3 erhalten wir  durch einsetzen von  x 3 in (4).

zu b) Die Steigung   der Geraden g ist in diesem Fall die Ableitung 

Indem man die Gleichung der Kurve implizit ableitet, erhält man   =

Rest   des   Beweises   ist   analog   zu   a).   Die   einzige   Ausnahme   stellt   dar,   dass  x 3 =  ² −2x 1 ist, da  x 1 offenbar doppelte Nullstelle ist. q.e.d.

Bemerkung 3

Offenbar ergibt sich jetzt als Ergebnis für PQ bzw.  PP  x 3 ,− y 3  .

Satz 2 Eine Elliptische Kurve  E ueber  ℝ ist zusammen mit der in Definition 3­5  erklärten Addition eine abelsche Gruppe Zu zeigen:

a) Abgeschlossenheit der Addition

b) Assoziativität

c) Kommutativität

d) Existenz des neutralen Elements

e) Existenz inverser Elemente

Seite 6 von 12

Page 7

Elementare Theorie Elliptischer Kurven

Zu a) Seien  P ,Q ∈ E .

Fall 1,  P = 0 :Nach Definition 5 ist  P  Q = Q und damit Element von  E . Fall 2,  P ,Q≠0  und  P = −Q : Nach Definition 5 ist  P  Q =  0 und damit  Element von  E .

Fall 3,  P ,Q≠ 0 mit  P= x 1, y 1  ,  Q= x 2, y 2  und  x 1 ≠x 2 . Nach Satz 1 ist der in Definition 3 erklärte Schnittpunkt  S  Element der Kurve, also  auch  −S = P  Q .

Fall 4,  P ,Q≠ 0 mit  P= x 1, y 1  , y 1 ≠ 0 und P=Q .

Nach Satz 1 ist der in Definition 4 erklärte Schnittpunkt  S Element der Kurve, also  auch  −S = P  Q .

Zu   b)   Der   Nachweis   der   Assoziativität   würde   den   Rahmen   dieser   Ausarbeitung  sprengen, es wird auf [2], [3], [4] verwiesen.

Zu c) Seien  P ,Q ∈ E .

Fall 1,  P = 0 : Nach Definition ist  0 Q = Q = Q  0  . Fall 2,  P ,Q≠0  und  P = −Q : Aus P = −Q folgt  −P = Q .  Also gilt nach Definition 5: P  Q = 0  = Q  P Fall 3,  P ,Q ≠ 0 mit  P= x 1, y 1  ,  Q= x 2, y 2  und  x 1 ≠x 2 : Da die Gerade durch   P und   Q gleich der Geraden durch Q und   P ist, ist  der   in   Definition   3   erklärte   Schnittpunkt   S in   beiden   Fällen   gleich,   also   auch 

Fall 4,  P = Q : Trivial.

Zu d) Sei  P ∈ E

Nach   Definition   5   gilt   P0 =P ,   folglich   ist   0 das   neutrale   Element   der  Elliptischen Kurve.

Zu e) Sei  P ∈ E

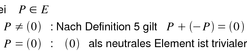
Fall 1,  P ≠ 0 : Nach Definition 5 gilt P  −P = 0  .

Fall 2,  P = 0 :  0 als neutrales Element ist trivialerweise das inverse Element  zu sich selbst. q.e.d.

Die Formeln aus Satz 1 definieren auch auf Elliptischen Kurven über jedem anderen  Körper   mit   Charakteristik   ungleich   2,3   in   sinnvoller   Weise   eine   Addition.   Dazu  folgende Plausibilitätsbetrachtung:

Wesentlich ist ja, dass der Punkt, den man durch Anwendung der Additionsformeln  erhält, selbst wieder ein Punkt auf der Elliptischen Kurve ist.

Seite 7 von 12

Page 8

Elementare Theorie Elliptischer Kurven

Die Formeln für die Addition sind im reellen Fall dadurch entstanden, indem wir nach  weiteren Lösungen der Gleichungen (4) und (5) gesucht haben. Wie wir auf (4) und  (5) gekommen sind (z.B. durch Differentialrechnung wie bei der Addition eines  Punktes zu sich selbst) ist ja nicht ausschlaggebend. Wichtig ist, dass die Lösungen  von (4) und (5) Punkte auf der Kurve sind.

Um zu zeigen, dass es genau eine weitere Lösung gibt und zum Ausrechnen dieser  Lösung haben wir als einzige Eigenschaft von  ℝ benutzt, dass  ℝ ein Körper ist.

Für Elliptische Kurven über Körpern der Charakteristik 2 oder 3 leitet man sich, von  den Gleichungen (2) und (3) ausgehend, ähnliche Formeln wie in Satz 1 her.

Man kann zeigen, dass diese Additionsformeln Elliptische Kurven über beliebigen  Körpern zu einer abelschen Gruppe machen 

4.Elliptische   Kurven   über   endlichen 

Körpern

In diesem Kapitel sei  GF  q ein endlicher Körper mit  q Elementen.

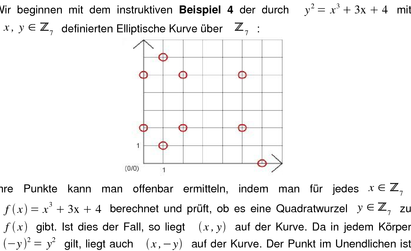
Wir   beginnen   mit   dem   instruktiven  Beispiel   4  der   durch   y ² = x ³  3x  4 mit 

Ihre   Punkte   kann   man   offenbar   ermitteln,   indem   man   für   jedes x ∈ ℤ 7  

ja auf jeden Fall enthalten.

Also   wird   man   keine   Elliptische   Kurve   über ℤ 7 finden,   die   mehr   als   2⋅7  1 Elemente besitzt

Seite 8 von 12

Page 9

Elementare Theorie Elliptischer Kurven

Fragt man nun nach der Elementezahl  N einer Elliptischen Kurve über dem Körper 

GF  q , so liefert uns die gerade angestellte Betrachtung folgende Abschätzung: 

Allerdings würde man vermuten, dass   N≈q ist, da in der multiplikativen Gruppe  eines endlichen Körpers nur die Hälfte der Elemente Quadratwurzeln besitzt. (Wir  folgen   der   Vorstellung,   dass   die   von f  x  = x ³  ax  b getroffenen  Körperelemente zufällig sind). Bei der Untersuchung dieser Vermutung helfen soll

Definition   6  Sei   GF  q ein   Körper   mit   q Elementen,   GF ^*  q die 

multiplikative   Gruppe   dieses   Körpers.   Der   quadratische   Charakter   von 

Für  x=0 definiert man   x =0 .

Wir könnn nun  N präzise angeben:

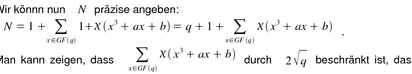
Man kann zeigen, dass   ∑

Resultat ist

Satz 3  (Satz von Hasse) Sei   N die Elementezahl einer Elliptischen Kurve über 

Einen Beweis dieses Satzes findet man z.B. in [5]

Nachdem die Frage der Elementezahl nun beantwortet ist, stellt sich als nächstes die  Frage nach der Struktur der abelschen Gruppe einer Elliptischen Kurve über einem  endlichen Körper. Dazu Beispiel 5

Seite 9 von 12

Page 10

Elementare Theorie Elliptischer Kurven

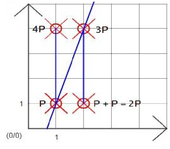
Zu sehen ist die durch  y ² = x ³  3x  2 gegebene Kurve über  ℤ 5 . Man sieht, dass   P=1,1 erzeugendes Element der Gruppe dieser Kurve ist, da  seine Vielfachen sämtliche Elemente der Gruppe durchlaufen ( 5P = 0 ist nicht  dargestellt). Folglich ist die Gruppe zyklisch.

Es stellt sich jedoch heraus, dass dies nicht bei jeder Elliptischen Kurve über einem  endlichen Körper der Fall ist. Jedoch ist die Gruppe einer Elliptischen Kurve über  einem   endlichen   Körper   in   jedem   Fall   das   Produkt   zweier   zyklischer   Gruppen  (genauer gesagt ist sie isomorph zu einem Produkt der Form ℤ /m ℤ×ℤ/n ℤ ).

Beispiel   6  Anhand   der   folgenden   Verknüpfungstabelle   der   durch   y ² = x ³  x

gegebenen Kurve über  ℤ 5 sieht man, dass ihre Gruppe nicht zyklisch ist, da jedes  Element zu sich selbst invers ist. Gegenübergestellt ist die Verknüpfungstabelle von 

ℤ /2 ℤ×ℤ/2 ℤ , die Isomorphie fällt sofort ins Auge.

Verknüpfungstabelle der Kurve

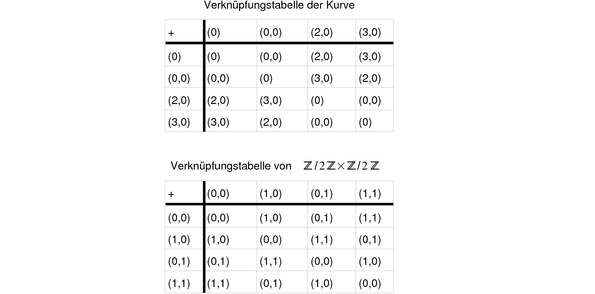
Seite 10 von 12

Page 11

Elementare Theorie Elliptischer Kurven

Wenn eine Elliptische Kurve  über   GF  q definiert ist,  ist  sie  ja auch  über  dem 

Erweiterungskörper  GF  q

Die Frage lautet nun: Wenn man die Elementezahl der Kurve über  GF  q kennt,  kennt man dann auch ihre  Elementezahl über  GF q Die Antwort liefert Satz 4

Sei  E eine elliptische Kurve über  GF  q .Die Elementezahl  N von  E über 

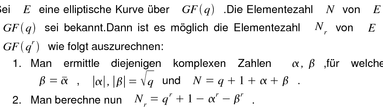
In   [1]   ist   erläutert,   wie   dieser   Satz   aus   der   inzwischen   bewiesenen   Weilschen  Vermutung folgt. Für einen Beweis der Weilschen Vermutung wird auf [5] verwiesen.

Wir demonstrieren das Verfahren aus Satz 4 am 

Beispiel 7 Die durch  y ² = x ³  3x  4 gegebene Kurve über  ℤ 7 ≃ GF 7 aus 

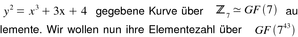
Beispiel 4 besitzt 10 Elemente. Wir wollen nun ihre Elementezahl über   GF 7 bestimmen.

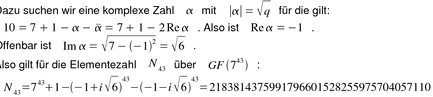
Dazu suchen wir eine komplexe Zahl   mit  ∣∣ = q für die gilt:

Offenbar ist  Im  =  7 − −1 ² =  6 . Also gilt für die Elementezahl  N 43 über  GF 7

Seite 11 von 12

Page 12

Elementare Theorie Elliptischer Kurven

5.Literaturverzeichnis

5.1.Quellen

[1] Koblitz, N., 1987, A course in Number Theory an Cryptography, New York.

Die   Visualisierungen   der   Elliptischen   Kurven   wurden   mit   Hilfe   der   auf http://www.elliptische­kurven.de erhältlichen Java­Applets erstellt.

5.2.Literatur

[2] Fulton, W., 1969, Algebraic Curves, New York

[3] Koblitz, N., 1984, Introduction to Elliptic Curves and Modular Forms, New York [4] Lang, S., 1978, Elliptic Curves: Diophantine Analysis, New York [5] Silverman, J., 1986, The Arithmetic of Elliptic Curves, New York

Seite 12 von 12