Excerpt
Page 1
Use of Stochastic Dominance to

Option pricing nowadays is a rather important topic. The most popular option pricing formula, developed by Black and Scholes [2], makes very strong assumptions to markets and the underlying security and is therefore not really applicable. In this paper we will introduce the theory of stochastic dominance as a tool for calculating option price bounds under more plausible assumptions.
1 Introduction
Since Black and Scholes [2] in 1973 published their article about option pricing there has been written a lot about this theme. Most of these articles made very restrictive assumptions namely markets were perfect and complete. To get a fair price under these assumptions one replicated the option by self-financing strategies. Black and Scholes for example derived the price with a continuously revised portfolio, however actual trading opportunities are discrete and therefore their crucial assumption limits the accuracy and applicability of the Black-Scholes model. As stated above this was done under very strong restrictions to markets and the distribution of the underlying security, due to this fact it is not very surprisingly that we observe deviations from this theoretical option value. Therefore it is necessary to develop a model which is able to explain the observed values and is more applicable in real existing markets. In this paper one of these more general models will be presented, namely stochastic dominance. In section two I will introduce the theory of preferences, expected utility and stochastic dominance and I will describe their relation. Unfortunately we do not get a unique price for the option value by relaxing the constraints but we get a range in which the option should quote. Some important papers concerning the theme of stochastic dominance are mentioned in section three where I will also give a short survey about their proceedings to derive option price bounds, these papers mainly deal with European options. A very intuitive idea was
Page 2
given by Constantinides and Perrakis [6]. For the most part my paper is based on their idea of observing a portfolio consisting of a risk free bond, a stock and a written option on this stock, so I will present their bounds in detail. They derived bounds for American cash-settled plain-vanilla put and call options, but as their bounds are very easily extended to European style options, we have a result applicable for the most common and often used types of options. In this model there are very little but reasonable assumptions made to the investors’ utility but none at all to the distribution of the underlying security. Moreover, they explicitly incorporated transactions costs and dividend payments for the call option bounds. After presenting their very general bounds there will be given some numerical examples for the special case of a lognormally distributed underlying in order to compare the derived bounds with the corresponding Black-Scholes price as the most popular model for calculating option prices. Additionally I will say a few words about the tightness and the empirical evidence of these bounds. As stated above the bounds were originally derived for plain-vanilla options but I will try to extend the bounds to a small class of exotic options what will be done in the last section.
2 The Theory
2.1 Preferences and Utility
We start with an individual or investor having some preferences on two random outcomes or here in our context two random payoffs belonging to two different investment decisions. Due to the random outcomes, let us denote them by X and Y , there are the following three possibilities for the investor to rank them:
(i) X Y , i.e. X is preferred to Y
(ii) Y X (or X Y ), i.e. Y is preferred to X,
(iii) X ∼ Y , i.e. the investor is indifferent between X and Y .
If we now moreover assume that these preferences satisfy some plausible properties it can be shown that they can be represented by a value function. This is very interesting since the expected utility preference relations belong to this class of preferences, where the value function is the expected utility. In other words it is possible to represent the preferences by the expectation of a utility function which was shown by von Neumann and Morgenstern (1944). This preference representation is the most widely accepted in finance and economics literature. This yields the following result where utility might be seen as a kind of monotone transformation
Page 3
of preferences:
X Y ⇔ E[u(X)] > E[u(Y )] (1)
But even if we are able to express the preference relation by an expected utility representation one has to define the utility function u. This is not an easy task and one easily sees that every positive monotone transformation of u can still represent the preferences which means that the utility function u is not unique. Therefore we are looking for tools to be able to state something about special classes of utility functions without knowing them explicitly. So we characterize the utility function u for a typology of investors and we obtain some useful results which hold within this typology of investors independent of the specific form of the utility function u.
Definition 2.1.1:
(i) Let U 1 represent the set of all non-decreasing utility functions u that possess a continuous first derivative.
(ii) Let U 2 represent the set of all non-decreasing utility functions u that possess a continuous first and second derivative, the second derivative being nonpositive.
(iii) Let U n represent the set of all utility functions u that possess continuous derivatives of at least order n ∈ N, with (−1) k u (k) (x) ≤ 0, k = 1, ..., n. 1
2.2 Stochastic Dominance
Definition 2.2.1 (First order stochastic dominance): Let X and Y be two random variables (outcomes). We say X dominates Y in the sense of first order stochastic dominance (FSD) if
F X (x) ≤ F Y (x), ∀x ∈ R (2)
and the inequality is strict for at least one x ∈ R, where F X (x) = P (X ≤ x) and F Y (x) = P (Y ≤ x).
Lemma 2.2.2: X dominates Y in the sense of first order stochastic dominance if and only if E[u(X)] ≥ E[u(Y )] with u ∈ U 1 . 2
The intuitive interpretation of this lemma is that given an investor with a nondecreasing utility function - which implies non-satiation - the expected utility of X
1 Here u (k) denotes the kth derivative of the utility function u.
2 For proof see Hadar [8]. Sometimes E[u(X)] ≥ E[u(Y )] with u ∈ U 1 is used for the definition of
FSD for the random variables X and Y . But with this lemma we get the equality of the definitions.
Page 4
is at least as large as the expected utility of Y if X dominates Y in the sense of FSD. As stated above in (1) the expected utility is a representation of the investors preferences and as assumption we observe investors belonging to the class of utility maximizers which in this case would therefore prefer X to Y . First order stochastic dominance is a very weak result and one will rarely be faced with such an obvious investment decision where the distribution function of one investment strategy is larger than the one of the other strategy. So we come to a more specific result by making the constraint that the utility function u moreover is concave which means u ≤ 0. This assumption is not very restrictive since it implies risk-aversion and decreasing marginal utility which is widely accepted as plausible. Finance and economic literature usually considers this class of utility functions. But first the definition of second order stochastic dominance.
Definition 2.2.3 (Second order stochastic dominance): Let X and Y be two random variables with distribution functions F X and F Y . We say X dominates Y in the sense of second order stochastic dominance (SSD) if
![]()
and the inequality is strict for at least one x ∈ R.
That means that the cumulated Probability that X ≤ t is smaller than the cumulated probability that Y ≤ t. Or to turn it around the cumulated probability that X > t is larger than the cumulated probability that Y > t, therefore we say X dominates Y .
Very similar to lemma 2.2.2 we get the following lemma for non-decreasing and concave utility functions u.
Lemma 2.2.4: X dominates Y in the sense of second order stochastic dominance if and only if E[u(X)] ≥ E[u(Y )] with u ∈ U 2 . 3
With this result for the SSD we are able to state something about the class of risk-averse investor with a non-decreasing utility function without knowing their utility functions explicitly. Namely we get that every out of this class maximizes his expected utility with X and prefers therefore X to Y if the cumulated distribution function of X is smaller than the cumulated distribution function of Y . The first and second order stochastic dominance are the most common and often used degrees, because they yield statements for very general and accepted classes of utility functions.
3 For proof see Hadar [8].
Page 5
However, sometimes it is not possible to ”find” stochastic dominance in the sense of first or second order. This is the case for FSD when the distribution functions and for SSD when the cumulated distribution functions intersect. 4 Nevertheless one can rank the random payoffs by using higher degrees of stochastic dominance. But as the degree of stochastic dominance increases the number of restrictions to the utility function increases and we get more special classes of utility functions which might be not really plausible. But of course, under more restrictions to the class of utility functions we will get tighter bounds for our option price. For the completeness here the definition of nth order stochastic dominance.
Definition 2.2.5 (N th order stochastic dominance): Let X and Y be two random variables with distribution functions F X and F Y . We say X dominates Y in the sense of nth order stochastic dominance (NSD) if for all x n ∈ R and n > 2, n ∈ N
![]()
and the inequality is strict for at last one x n ∈ R.
Again we get a relation between dominance of n-th order stochastic dominance and the expected utility for a class of utility functions.
Lemma 2.2.6: X dominates Y in the sense of nth order stochastic dominance if and only if E[u(X)] ≥ E[u(Y )], ∀u ∈ U n .
Remark 2.2.7: If X dominates Y in the sense of nth order stochastic dominance then X dominates Y in the sense of (n + 1)th stochastic dominance.
What have we done in this section. We pointed out, that the investor’s preferences can be described by the expected utility. And moreover, I showed that the stochastic dominance is a tool for ranking expected utility for very general classes of utility functions. All together we have seen that if X dominates Y in the sense of stochastic dominance then the expected utility of X is larger than the expected utility of Y and therefore the investor would prefer X to Y if he belongs to the class of utility maximizers.
4 For example see appendix.
Page 6
3 Option Bounds
From now on we are interested in reasonable bounds for option prices. Of course, there are some natural bounds for option prices resulting from arbitrage arguments. For example for an American call option. Obvious an American call option always should be worth more than [S t − K] + . Since, if the price of the claim felt below [S t − K] + there would be an arbitrage opportunity and one could make money from buying the call option and immediately exercise it. But these kinds of bounds are very general as result not tight and therefore more or less useless. What we are looking for are bounds which are as tight as possible without making implausible restrictions. Above I introduced the theory of stochastic dominance which will be used to derive some bounds. There are many articles about the use of stochastic dominance to bound option prices under less restrictive assumption than made in models with equilibrium prices.
In 1984 Perrakis and Ryan [15] published their article about option pricing bounds in incomplete markets where trading opportunities are discrete and not continuous. By the law of one price and arbitrage arguments they developed single and multiperiod bounds for European call and put options using the Rubinstein approach for current asset prices. These bounds were compared by Ritchken [16] (1985) who found bounds for option prices in incomplete markets using single-period linear programming. This means that a linear program is established to search arbitrage opportunities over a number of portfolio strategies. It was shown that with further assumptions on preferences and state probability Ritchken’s upper bound equals the upper Perrakis-Ryan bound whereas the lower bounds differ. Also Levy [14] in 1985 developed upper and lower bounds for unconstrained and concave utility functions by applying the theory of stochastic dominance, namely FSD for unconstraint and SSD for concave utility functions. His bounds which were identical with these of Perrakis and Ryan were derived by observing any combination of stock and risk less asset and comparing it with any combination of call and the risk less asset of the same cost in bullish and bearish markets. In 1988 Ritchken and Kuo [17] generalized the single-period linear programming bounds on option prices and allowed for a finite number of revisions. These bounds were derived by using a modified binomial option pricing model and under restrictive assumptions than Perrakis and Ryan made they got even tighter bounds. Higher orders of stochastic dominance were derived by Ritchken and Kuo [18] 1989 who made the explicit assumption of decreasing absolute risk aversion (DARA). To use third or even higher order stochastic dominance one has to make further assumptions to the utility function. This was done by Ritchken and Kuo who also showed that as the order of stochastic dominance increases additional constraints (which might be restrictive and not plausible) must be added but of course the bounds get tighter. Basso and Pianca [1] 1997 also derived higher order stochastic dominance bounds and got very efficient bounds for third
Page 7
order stochastic dominance. But as their objective function is no more linear their program is very difficult to implement and therefore, unfortunately, not very useful. In 2002 Constantinides and Perrakis [4] derived SOD bound for European put and call options in markets with discrete trading opportunities and even proportional transaction costs. Again these bounds made plausible assumptions to utility functions and where independent of the distribution of the underlying security. Ryan in 2003 tried to improve the SSD bounds and used therefore the observed price of the concurrently expiring options with the closest exercise price to the initial option for which the bounds are to be found. But his resulting options were not very tight and Huang [11] 2004 improved these bounds by making use of n concurrently expiring options instead of only one like Ryan did. Moreover Huang [12] extended these bounds for stochastic dominance of nth order. One of the very general models using SSD which incorporates discrete trading and even explicitly proportional transaction costs and dividend payments was the extension of Constantinides and Perrakis [6] 2004. Their new model will now be presented as an example in detail, because it is as stated above very general and does not assume a specific distribution of the underlying asset. Moreover the bounds are derived for American call and put options, from which bounds for European options as special case are easily obtained. All together we afterwards have bounds for the most common option types, namely American and European style plain-vanilla put and call options.
3.1 The Model of Constantinides and Perrakis
The option bounds I will present in this section were derived by Constantinides and Perrakis [6]. Therefore I will show their results, namely the bounds, and skip their proofs which are very technical. So the proofs of the following propositions can be found in [6] and I will skip the proofs of the corollaries, which follow straight forward. In this model we observe a trader holding a portfolio consisting of two primary assets, namely a risk less bond and a risky stock. The trader may have long or short positions in these two assets. Furthermore we assume the existence of a class of utility maximizing traders but we do not assume all traders to behave as such. From now on by trader one out of the class of utility maximizers is meant. Each of these traders are allowed to make sequential investment decisions in the two primary assets at dates t, t = 0, ..., T < ∞ where T denotes the terminal date at which his positions get closed.
Let now {γ t } t=1,...,T (0 ≤ γ t < 1) be the sequence of the deterministic dividend yields which are known to the trader at date t = 0. We then define (1 + γ t )S t as the cum dividend stock price, γ t S t as the cash dividend and S t as the ex dividend stock price. It makes sense to assume that S 0 is larger than zero and that the rate of return of the stock is positive but finite that means (1 + γ t+1 ) S t+1 ∈ [0, ∞) Moreover
St
we make the assumption that the rates of return are independently distributed with
Page 8
conditional mean
![]()
Without loss of generality we assume the existence of a bond with price one at the initial date t and R > 1 at t + 1, R is assumed to be constant over time. Trading in the bond does not incur transaction costs whereas trading in the stock causes proportional transaction costs which are charged to the bond account. That means that the trader has to pay (1 + k 1 )S t for buying a share of stock at date t and he is credited (1 − k 2 )S t for selling or shorting a share of stock at t. The transaction cost parameter k 1 for buying shares and k 2 for selling (shorting) shares are restricted to lie in the interval of [0, 1) what awfully makes sense. If the ki was not within the interval, then we would either get money for trading (k i < 0) or we would have to pay more transaction costs than the shares we wanted to trade in are actually worth (k i ≥ 1). Now it is possible to define the conditional mean return with reinvested dividends net of transaction costs, as
![]()
The distinction between R T AC and R t is only the incorporation of transaction
t
costs but in practice where dividend yield and transaction costs only are a few percent one do not have to distinguish between them. We consider now a trader entering the market at date t with holdings in the bond account and some shares of stock. Constantinides and Perrakis then introduced a decision variable for the trader to change his positions in the bond account and the stock holding at each date t to maximize his expected utility at the end of his horizon which is at date T . Therefore they defined a recursive value function. The decision variable makes sure that we observe a self-financing strategy and so get stochastic dominance as increasing the expected utility by adopting a zero-net-cost strategy. On first sight this might remind of arbitrage but be very careful, since arbitrage is risk free whereas the expected utility or stochastic dominance takes risk into account. Of course we defined here utility over the net worth and not consumption as usually done, but as we assume that the consumption as a function of wealth is increasing we get the same result. Furthermore we need the assumption of an increasing and concave utility function u to employ the second order stochastic dominance.
3.2 Put Option Bounds
In this section I will present the lower and upper bounds for American and as special case for European plain-vanilla put option which were derived by Constantinides and
Page 9
Perrakis [6]. To be exact the presented bounds are for the reservation purchase price of an option which is the maximum price below which any trader increases expected utility by purchasing the option. These bounds were derived for cash-settled options with strike price K and expiration date T ≤ T . One simplifying assumption was made with respect to the stock, namely that no dividends were paid over the options life time, therefore γ t = 0 ∀t ∈ {0, ..., T }.
Now we observe a trader at date t with the two primary assets and a long position in a put option. The trader is constrained from selling the option, so he only is allowed to hold the option or to exercise it. Where the cash payoff of exercising the option at date t ≤ T is K − S t . Constantinides and Perrakis therefore again defined recursively a value function to moreover maximize the expected utility at the end of the traders horizon T over the two possibilities the trader has, namely exercising the option or hold the option. This is rather technical and in detail only necessary for the proof of the following propositions therefore it will be skipped and is to be found in [6]. By this we get that one of these decisions is linked to a larger expected utility which is nothing else than stochastic dominance as shown in lemma 2.2.2 for FSD and in lemma 2.2.4 for SSD. Their assumptions to utility functions rely on SSD and with other words we observe utility functions u within U 2 . For this class of utility function Constantinides and Perrakis obtained the following results:
Proposition 3.2.1: At time t ≤ T
![]()
is a lower bound on the reservation purchase price of an American put option. Where for S ≥ 0, M (S, t) is recursively defined as
![]()
M (S, t) =
Straight forward we come to a lower bound for a European put option as a European put option can be interpreted as an American put option with the constraint of not exercising the option until date T which is the maturity date of the option.
![]()
T
−1
In this case we get that M (S, t) = therefore:
Corollary 3.2.2: At time t ≤ T

P E (S t , t) =
Page 10
is a lower bound on the reservation purchase price of a European put option.
In this special case it is very easy to adjust the derived bound for dividends paid on the stock, one only has to replace R s by R T AC . Furthermore it is possible to
s
tighten the bound even more by assuming that there is at least one trader having an investment horizon ending at the maturity date of the option, that means for this trader T = T .
Proposition 3.2.3: At time t ≤ T = T
P A (S t , t) = max {K − S t , M (S t , t)} (9)
is a lower bound on the reservation purchase price of an American put option. M is defined as above.
Corollary 3.2.4: At time t ≤ T = T

is a lower bound on the reservation purchase price of a European put option.
And as above one has to replace R s by R T AC for an adjustment to a dividend
s
paying stock. We now have lower bounds for American as well as European option prices and so come to the upper bounds.
Proposition 3.2.5: At time t ≤ T
P A (S t , t) = max {K − S t , L(S t , t)} , t ≤ T (11)
is an upper bound on the reservation write price of an American put option. Where L(S t , t) is recursively defined as L(S t , t) =
−
(1−k
2
)K

10
Page 11
Corollary 3.2.6: At time t ≤ T

P E (S t , t) =
is an upper bound on the reservation write price of a European put option.
As we did above we make the assumption that there exists at least one whose investment horizon coincides with the option’s maturity date T . In this case the transaction costs in Proposition 3.2.5 disappear only for t = T − 1. Whereas we for the reservation write price of a European put option get:
Corollary 3.2.7: At time t ≤ T = T

P E (S t , t) =
is an upper bound on the reservation write price of a European put option.
3.3 Call Option Bounds
Very similar to deriving bounds for American and as special case for European put options we now observe a trader with positions in the two primary assets and a short position in an American cash settled call option on the stock. As the trader has a short position in the option, the derived bounds in this section are for the reservation write price of an option which is the minimum price above which any trader increases expected utility by writing the option. We permit dividend paying of the stock during the options life as a simplifying assumption. The difference is that the trader now has a short position in the option which means that he is not able to choose if he exercises the option or not but he is dependent of the decision of the option holder he is assigned to. Therefore the value function in this section is defined as the trader’s expected utility under his personal worst-case scenario.
Proposition 3.3.1: At time t ≤ T

Page 12
is an upper bound on the reservation write price of an American call. Where N (S, t) is defined as N (S, t) =
![]()
For a European call option again N (S, t) simplifies to
![]()
T
−1
N (S, t) =
Corollary 3.3.2:

C E (S t , t) =
is an upper bound on the reservation write price of a European call.
And finally there is a lower bound on the reservation purchase price of an American call to be calculated. The price of an American option is always higher or equal the price of the corresponding European option. This is the fact because an American can be exercised during the whole life time and therefore one has to pay a premium. So the lower bound for a European option is always a lower bound for an American option. In this case the lower bound for an American call even equals the lower bound for a European call, since it is never optimal to exercise an American call before the maturity date T due to the interest disadvantage by paying the strike price early. With the put-call parity −P t + C t = S t − KR −(T −t) we obtain from corollary 3.2.4:
Proposition 3.3.2: At date t ≤ T = T
C E,A (S t , t) =
![]()
is a lower bound on the reservation purchase price of a European and an American call option.
We now have for all types of plain-vanilla options their upper and lower bounds given by Constantinides and Perrakis (2004) and now are ready for a few numerical results to state something about the tightness and the resulting applicability of their bounds to financial markets.
Page 13
3.4 Numerical Results
All presented proceedings are numerically to be solved. As mentioned above Constantinides and Perrakis for example used a lot of recursively defined functions. And for their bound I will in this section show a numerical example. In order to have a relative value, these bounds are calculated under the assumption of a lognormally distributed underlying security. So we are able to calculate the corresponding Black-Scholes price for American options which not very surprisingly lies within the calculated range.
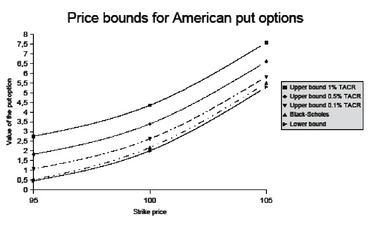
As example here are presented the calculated bounds for an American cashsettled put option, where we assume a stock price S t of 100, an annual expected stock return of 8% and an annual volatility of 20%. The options maturity date T is in one month and the risk free rate equals 3%. Proposition 3.2.1 is used to calculate the lower bounds and the upper bounds are calculated with the formula given in proposition 3.2.5. Moreover these bounds are calculated as a function of the transaction cost rate (TACR) and the strike price K.

Right from this table one might see that the lower bound is really tight and unaffected by changes in the transaction cost rate. On the other hand the upper bound is not tight and becomes even less tight when the transaction cost rate increases. To illustrate these results more obviously I included the graph below which containes the calculated bounds and the correspomding Black-Scholes price for American options.
There exists a lot of literature about the topic of stochastic dominance but, however, most of them calculate the corresponding bounds and compare them only to the Black-Scholes (American) value. Unfortunately very less literature is to be found about the empirical evidence of these bounds with observed option prices. One paper about this topic was written by Constantinides, Jackwerth and Perrakis [5]. They investigated the mispricing of index future options and found that there are worth mentioning violations of the Constantinides and Perrakis (2002) bounds. With other words there existed possibilities for all risk-averse traders to increase their expected utility by adopting a zero-net-cost strategy.
Page 14
4 Extension to Exotic Options
We now have seen the bounds derived by Constantinides and Perrakis for both plainvanilla American and plain-vanilla European options. But even if those bounds were originally derived for plain-vanilla options it is possible to extend their work to a class of similar exotic options. For example one can very easily extend it to a special case of the so called chooser option. The owner of this contingent claim is allowed to decide at a specific date during the options life time whether his option will be a put or a call option, the strike for both is in most cases the same. If we now observe the double special case of a European style chooser option where the owner has to decide between call an put option at the date of maturity, then the option is nothing else but a straddle, which is an option strategy buying a put and a call with the same strike. By the law of one price the option has to have the same price as the straddle and we get a lower bound by summing up the two lower bounds and an upper bound by summing up the upper bounds for the European plain-vanilla put and call. Unfortunately this range will not be very tight but it is a criterion. Another example might be the Bermuda option, which is a mixture of a European and an American style option where the owner is allowed to exercise the option on several fixed dates during the options life time. For example he might be allowed to exercise on every first of the month. A Bermuda option can be a put or a call and we could use the derived bounds by making the restriction that it is only possible to exercise the option on dates t coinciding with the fixed exercising dates of the option. Constantinides and Perrakis in their paper also used their bounds for index future options as the stock as risky asset can be replaced by an index or even by a stock basket these bounds are useful for rainbow options which are options on a stock basket.
Page 15
But of course there are several kinds of exotic options which are very difficult to handle. One of these examples is the Asian option which also sometimes is called average option. This contingent claim is structured like a plain-vanilla but the difference is that the strike price equals the average value of the underlying security
![]()
over the life time. Therefore the strike price K = 1
describes the i-th stock price observed during the options life time. The problem of this option is that the distribution of the sum of lognormal distributed random variables is not elementary. Very similar to Asian options are the so called lookback options. In this case the strike price K equals the minimum of the stock price during the options life time for a call and the maximum of the stock price for a put. The
![]()
payoff of a lookback put option is max
S
T
−
min
0≤t≤T
investigations of option pricing bounds.
Page 16
5 References
[1] Basso A. and P. Pianca (1997). ”Decreasing Absolute Risk Aversion and Option Pricing Bounds.” Management Science 43.
[2] Black, F. and M. S. Scholes (1973). ”The Pricing of Options and Cor-porate Liabilities.” Journal of Political Economy 81, 637-654
[3] Brealey, R. A. and S.C. Myers (2000). ”Principles Of Corporate Finance.” 6th edition, McGraw Hill.
[4] Constantinides, G. M. and S. Perrakis (2002). ”Stochastic Dominance Bounds on Derivatives Prices in a Multiperiod Economy with Proportional Transaction Costs.” Journal of Economic Dynamics and Control 26, 1323-1352
[5] Constantinides, G. M. , J. C. Jackwerth and S. Perrakis (2003). ”Mispricing of S&P 500 Index Options.” Working paper, University of Chicago, University of Konstanz, Concordia University.
[6] Constantinides, G. M. and S. Perrakis (2004). ”Stochastic Dominance Bounds on American Option Prices in Markets with Frictions.” Working paper, University of Chicago and Concordia University.
[7] De Giorgio, E. (2002). ”Reward-Risk Portfolio Selection and Stochastic Dominance.” Working paper, University of Zurich.
[8] Hadar, J. and W. R. Russell (1970). ”Stochastic Dominance and Diversification.” Journal of Economic Theory 3, 288-305.
[9] Henin, C. and N. Pistre (1997). ”The Use of Second-Order Stochastic Dominance To Bound European Call Prices: Theory and Results.” Numerical Methods in Finance, 305-326.
[10] Heyer, D. D.. ”Stochastic Dominance: A Tool for Evaluating Reinsurance Alternatives.”
[11] Huang, J. (2004). ”Option Bounds and Second Order Arbitrage Opportunities.” Working paper, Lancaster University.
Page 17
[12] Huang, J. (2004). ”Stochastic Dominance Option Bounds and N th Order Arbitrage Opportunities.” Working paper, Lancaster University.
[13] Kohlmann, M. (2004). ”Stochastik III, Mathematics Meets Finance.” University of Konstanz
[14] Levy, H. (1985). ”Upper and Lower Bounds of Put and Call Option Value: Stochastic Dominance Approach.” Journal of Finance 40, 1197-1217.
[15] Perrakis, S. and P. J. Ryan (1984). ”Option Pricing Bounds in Discrete Time.” Journal of Finance 39, 519-525.
[16] Ritchken, P. (1985). ”On Option Pricing Bounds.” Journal of Finance 40, 1219-1233.
[17] Ritchken, P. and S. Kuo (1988). ”Option Bound with Finite Revision Opportunities.” The Journal of Finance 43.
[18] Ritchken, P. and S. Kuo (1989). ”On Stochastic Dominance and Decreasing Absolute Risk Averse Option Pricing Bounds.” Management Science 35, 51-59.
[19] Yamai, Y. and T. Yoshiba (2002). ”Comparative Analyses of Expected Shortfall and Value-at-Rick (2): Expected Utility Maximization and Tail Risk.” Monetary and Economic Studies.
Page 18
Appendix
In the first plot obviously no random variable dominates the other in the sense
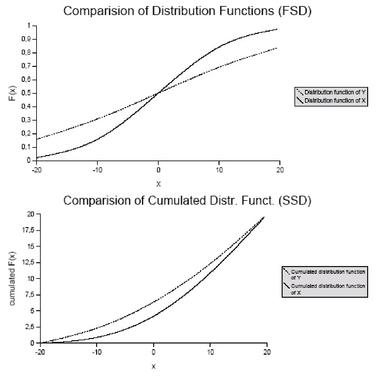
of first order stochastic dominance. Therefore we are not able to rank the random outcomes with respect to this order of dominance. But in the second plot one sees that X dominates Y in the sense of second order stochastic dominance and so we are able to rank the random outcomes by second order stochastic dominance. If now even graphs of the cumulated distribution functions intersect one has to look for stochastic dominance of higher order.
- Quote paper
- Benno Günther (Author), 2005, Use of Stochastic Dominance to Bound Option Prices, Munich, GRIN Verlag, https://www.grin.com/document/109514
Publish now - it's free






















Comments