Kombinatoren für die Breitensuche

Page 1

Referentin: Hermine Reichau Proseminar : Funktionale Programmierung Thema des Vortrags : Kombinatoren für die Breitensuche Bezogener Text: ‚Combinators for breadth-first search’ von Michael Spivey,

Inhaltsverzeichnis

1. Ergebnisräume multipler Funktionen

2. Breitensuche

3. Kompositionen

4. Assoziativität von join

5. Infopapier zu den verwendeten Operationen

Hermine Reichau

Prof.Dr.M.Schmidt-Schauß/ M.Mann

Proseminar: Funktionale Programmierung

14.06.2002

Page 2

Kombinatoren für die Breitensuche

1. Ergebnisräume multipler Funktionen

Der ein oder andere hat sicherlich bereits festgestellt, dass es Funktionen gibt, welche neben einer Reihe erfolgreicher Berechnungsergebnisse zusätzlich eine Anzahl von Berechnungsfehlschlägen zurückgeben. Dies lässt sich umgehen, indem man sich von diesen multiplen Funktionen ¹ eine Liste der erfolgreichen Berechnungen zurückgeben lässt. Allerdings kann es passieren, dass diese Listen leer sind oder, was weitaus schlimmer ist, dass sie nicht terminieren. Das Generieren dieser Erfolgslisten ist vergleichbar mit der unvollständigen Tiefensuche in Prolog; wir werden gleich am Beispiel der Faktorensuche zu einer gegebenen Zahl n sehen weshalb.

Die Lösung für dieses Problem erscheint zunächst einfach: Wissen wir, dass uns eine Funktion entweder kein Ergebnis oder unvorhersagbar viele Ergebnisse zurück gibt, so ersetzen wir diese durch eine genuine Funktion welche uns einen lazy stream zurückgibt: Angenommen, wir möchten zu einer frei gewählten Zahl n alle Paare von Faktoren herausfinden, welche miteinander multipliziert gerade das Produkt n ergeben. Deshalb nehmen wir alle möglichen Faktoren und fassen sie jeweils zu Paaren zusammen, so dass jeder Faktor mit jedem Faktor kombiniert wird, und daraufhin getestet wird ob das Produkt eines Paares n ergibt. Wenn das der Fall ist, war der Test erfolgreich und das Paar wird in eine Ergebnisliste eingetragen, andernfalls wird das Paar fallen gelassen. Unter bestimmten Umständen kann es aber sein, dass eine solche Ergebnisliste entweder leer bleibt oder aber divergiert.

Eine Funktion die eventuell eine unendliche Anzahl von Berechnungsschritten und Ergebnissen hervorruft, kann nicht allein durch endliche Listen implementiert werden. Daher müssen wir unterscheiden zwischen finiten Listen (α list) und Listen die potentiell infinit sein können. Diese Listen werden als lazy ² streams (α stream) bezeichnet. Beide Listentypen werden auf die gleiche Weise implementiert. Gegeben seien zwei Funktionen f und g mit: (1) f :: α → β stream (2) g :: β → χ stream χ α → ∧ :: stream f g Die Komposition dieser Funktionen ist gegeben durch .

Weiterhin sei g*=map g, d.h. g wird auf jedes Element seiner Argumentenliste angewendet und das Ergebnis der Anwendung wird in einen neuen Stream geschrieben. Die Argumentliste von g ist aber bereits ein Stream, der zuvor mit (1) durch f erzeugt wurde. Daher beschreibt g* eine Funktion vom Typ: β stream → (χ stream) stream g ∧ kann also definiert werden durch: Die Komposition f

¹ multipel deshalb weil sie mehr als ein Ergebnis zurückgeben

² Diese Listen werden mittels ‘lazy evaluation’ ausgewertet, das heißt, ein Ausdruck oder Teilausdruck wird nur berechnet, wenn es unbedingt nötig ist, und dann auch nur einmal.

Page 3

g ∧ = ⋅ ⋅ * f f g concat

Äquivalent dazu lässt sich der Kompositionsoperator ∧ wie folgt definieren: = ∧  ← ← z x f g [ ) ( ] ; gy z fx y Behauptung

Der Kompositionsoperator ist assoziativ. ⁴ ∧ ∧ = ∧ ∧ ) ( ) ( f g h f g h Zu zeigen: . Voraussetzung ⋅ = ⋅ (a) * * * h concat concat h ⋅ = ⋅ (b) concat concat concat concat * ⋅ = ⋅ (c) * * )* ( p q p q Beweis ∧ ∧ ) ( f g h ^∧ ⋅ ⋅ ⋅ ⋅   →  def * ) * ( f g h concat concat ⋅ ⋅ ⋅ ⋅ →  ) ( c * * * * f g h concat concat ⋅ ⋅ ⋅ ⋅ →  ) ( b * * * f g h concat concat ⋅ ⋅ ⋅ ⋅ →  ) ( a ) * ( * f g concat h concat ^∧ ∧ ∧   →  def ) ( f g h

Zurück zu dem Faktorisierungsproblem am Anfang. Zunächst benötigen wir eine Funktion, die eine vorgegebene Liste potentieller Faktoren für eine Zahl n so erweitert, dass letztendlich alle möglichen Paare von Faktoren gebildet werden. Die Ergebnisse sollen uns als lazy stream übergeben werden.

Wir definieren die Funktion vom Typ choose:: int list → (int list) stream mit choose xs = [xs++[x]|x ←[1…]]

Haben wir die nötigen Elemente ausgewählt wollen wir testen, ob sie Faktoren von n sind. Dies testen wir mit der Funktion test n. Falls das getestete Paar miteinander multipliziert n ergibt, wird es als [x,y] zurück gegeben und in einen Stream aus Listen geschrieben, andernfalls wird nichts [] zurückgegeben. Die Funktion test ist also vom Typ test:: int → int list→( int list ) stream und wird definiert durch x = ⋅ test n[x,y] = if n y then[[x,y]] else[]

Hieraus lässt sich nun eine Funktion zusammensetzen welche nach Faktorenpaaren einer gesuchten Zahl n sucht: ∧ ∧ factorize n = )[] ( choose choose n test

Diese Funktion arbeitet folgendermaßen:

Das rechte choose wird auf die leere Argumentliste[] angewendet, so dass wir hieraus eine Liste aus Listen gewinnen, die jeweils ein einziges Element haben. Es wird theoretisch der stream [[1],[2],[3]...] erzeugt. Da wir streams aber mittels lazy evaluation auswerten wollten, wird zunächst einmal nur das erste Element ausgewertet, indem es an das linke choose übergeben wird. Dieses kombiniert nun alle möglichen Faktoren mit dieser [1], so dass

³ Zunächst wird die Funktion f auf x angewendet, woraus wir y erhalten. g wird dann auf y angewendet woraus wir schließlich z erhalten.

⁴ Das muß er sein, damit die Funktionen die diesen Komparator verwenden eindeutig sind. Siehe hierzu auch Seite 7 unten.

Page 4

folgender Stream erzeugt wird [[1,1], [1,2], [1,3],...,[1,59], [1,60], [1,61]...]. Direkt nach der Erzeugung eines Paares, wird das Paar von der Funktion test ausgewertet. Nehmen wir n = 40 an, dann würde der Ergebnisstream nur einen einzigen Eintrag erhalten, nämlich [[1,40]]. Danach würde factorize divergent weitere Paare mit 1 als erstem Element hervorbringen und niemals zu 2 als erstes Element gelangen. Die einzige Lösung die dieses Programm findet ist [[1,n]].

Ein äquivalentes Verhalten zeigt folgendes Prologprogramm: factorize(N,X,Y) :- choose(X), choose(Y), X*Y= :=N

Auch hier wird X=2 niemals erreicht, da Prolog Probleme über Tiefensuche verarbeitet.

2. Breitensuche

Ein effektiverer Ansatz um das Faktorisierungsproblem zu lösen ist der, nicht nacheinander jedes x mit allen möglichen y zu Paaren zusammenzufassen und dann zu x+1 überzugehen, sondern parallel alle möglichen x mit allen möglichen y zusammenzuschließen. Wir initialisieren hierfür einen Baum der zunächst die möglichen x abträgt:

Mit jedem Blatt wird ein Index verknüpft, der angibt, wie viele Auswahlschritte gebraucht wurden um es zu erreichen. Wir legen fest, dass der Index für die Auswahl von [n] gleich n-1 ist.

In unserem Faktorisierungsprogramm werden zwei Auswahlen hintereinander getroffen: choose ∧ choose . Um dies zu veranschaulichen erweitern wir den bereits vorhandenen Baum, indem wir an jedes Blatt eine Kopie des Baumes einfügen der durch das zweite choose generiert

[1,1]

der Auswahlschritte eines Paares.

Wenn wir nun nach in Frage kommenden Faktoren suchen, möchten wir möglichst alle Paare finden und das in einer akzeptablen Zeit. Eine Tiefensuche würde sich hier in einem der noch

Page 5

immer infiniten Teiläste des Baumes verlieren, während Blätter in anderen Teilästen unbesucht blieben. Besser geeignet ist hier offensichtlich eine Breitensuche. Die Breitensuche sucht ihrer Natur nach in der Reihenfolge, die der Index vorgibt, das garantiert, dass wir nach und nach jeden Ast mit jedem Blatt besuchen. Auf diese Weise wird der Baum Ebene für Ebene abgearbeitet.

Um diese Idee umzusetzen ist es notwendig, nicht nur alle potentiellen Faktorenpaare in einem Stream zu sammeln, sondern, um die Baumstruktur nachzuempfinden, muss jedes Faktorenpaar mit seinem Index verbunden werden. Dies leistet der Stream, den wir zu Anfang verwendet haben, nicht mehr. Daher definieren wir uns hier einen neuen Typ, der dieses leisten kann: matrix α =(α list) stream

Hierbei handelt es sich um einen infiniten stream, der finite Listen zum Inhalt hat. Jede Liste enthält alle potentiellen Faktorenpaare mit dem gleichen Index. Auf diese Weise werden die Paare Zeile für Zeile zusammengefasst wobei jede Zeile einen anderen Index repräsentiert. Anders als bei herkömmlichen Matrizen, hat unsere Matrix jedoch eine unendliche Anzahl von Zeilen und die Länge der Zeilen variiert. Beispiel:

Für unseren Baum oben erhalten wir in etwa folgende Matrix: Index Listeninhalt

0 1 2 3

Die Funktionen choose und test müssen neu definiert werden, um den Matrix-Typ zu implementieren. Von choose möchten wir gerne einen stream mit finiten Listen zurück bekommen, so dass jede Liste eine einzige Auswahl enthält: choose xs = [[xs ++[x]]x ← [1…]]

Von test erwarten wir nun ebenfalls einen Stream aus Listen: x = ⋅ n y test n [x,y] = if then [[[x,y]]] else []

Mit diesen Hilfsdefinitionen lässt sich nun unser Faktorisierungsprogramm modifizieren: ∧′ ∧′ = )[] ( choose choose n test n factorize

Hiermit müssten sich also alle Faktorenpaare von n finden lassen. Allerdings terminiert die Berechnung noch immer nicht, da es ja selbst nachdem es alle Faktorenpaare gefunden hat weiter Ebene für Ebene durchsucht und es ja unendlich viele Ebenen gibt. Auf den unteren Ebenen werden nur noch leere Listen zurück gegeben. Solange also unser Suchraum infinit ist lässt sich dieses nicht vermeiden. Wir benötigen also einen begrenzten Suchraum und einen modifizierten Algorithmus der auf ihm arbeitet. 3. Kompositionen

Page 6

∧ eigentlich leistet. Was wir Bisher ist offen geblieben, was der neue Kompositionsoperator ' bisher voraussetzen ist, dass er mit den neu definierten Typen kompatibel ist. Was uns fehlt, ist zum einen eine Definition dieses Operators und die Gewissheit, dass er assoziativ ist. Assoziativ muss er sein damit so ein Programm wie factorize n eindeutig sein kann.

Gegeben sei eine unbekannte Funktion vom Typ join :: (α matrix)matrix → α matrix. Diese Funktion ist also ähnlich wie die Funktion concat, welche auf Listen funktioniert. ∧ äquivalent zu unserem alten Operator ∧ definieren als: Wir können nun ' ⋅ ⋅ = ∧ mit g**::β matrix → (χ matrix)matrix f g join f g * * '

und f ::α → β matrix ; g ::β → χ matrix

Wenn es diese Funktion join geben sollte, so müsste es relativ einfach sein, Assoziativität für ∧ nachzuweisen, und zwar mit den gleichen Argumenten wie schon gezeigt. '

Auf der Suche nach einer geeigneten Definition für join, halten wir nach ein paar nützlichen Hilfsfunktionen Ausschau, aus denen wir schließlich join zusammensetzen können. Voraussetzung: alle potentiell infiniten streams sind tatsächlich infinit, so dass nicht auf die Möglichkeit Rücksicht genommen werden muss, dass sie eventuell doch terminieren. Da matrix α = (α list)stream, kann es nützlich sein, über eine Funktion vom Typ (α stream)list → (α list)stream zu verfügen. Diese kann definiert werden als ein fold auf Listen trans[] = repeat [] trans(xs:xss) = zipWith(:)xs(trans[]) 5

Diese Funktion nimmt also eine Liste in der streams enthalten sind. Von jedem stream nimmt sie das erste Element (head) und schreibt alle ersten Elemente in eine Liste (nach Reisverschlussprinzip), danach wird das ganze mit dem zweiten und jedem weiteren Element wiederholt, da wir zu Anfang eine Liste aus Streams haben, erzeugen wir auf diese Weise einen Stream aus finiten Listen. Das heißt, wir können trans alternativ auch wie folgt definieren:

trans xss = (head*xss):(trans(tail*xss)) Anschaulich macht diese Funktion also folgendes:

trans[[x 00 , x 01 , x 02… ], [x 10 , x 11 , x 12 …], [x 20 , x 21 , x 22 …]…[x (n-1)0 , x (n-1)1 , x (n-1)2… ]]

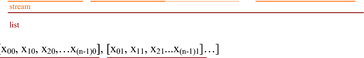
= [[x 00 , x 10 , x 20 ,…x (n-1)0 ], [x 01 , x 11 , x 21 ...x (n-1)1 ]…]

list

stream

Das Ergebnis ist eine Matrix mit infiniter Zeilenanzahl. Für join wünschen wir uns, dass es folgendes leistet: (α matrix)matrix → α matrix. Mit der Typdefinition α matrix =(α list)stream erhalten wir daraus: join :: (((α list)stream)list)stream → (α list)stream Dann können wir mit trans folgende Komposition für join definieren:

⁵ also gilt für trans als fold-Operation: trans = foldr(zipWith(:))(repeat[ ] )

Page 7

α      →    →  * concat concat trans LS LLSS LSLS ( L= Liste, S= Stream) S L ^. Mit concat L concat S = concat L * ^. concat S = concat S concat L ** ⁶ Wobei concat L auf Listen ausgeführt wird und concat S auf streams.

Diese Definition für join hat aber leider einen Haken: Die Ergebnisse müssen ihrem Index nach aufsteigend geordnet sein. concat S kommt dieser Notwendigkeit nicht nach. Daher brauchen wir noch weitere Hilfsfunktionen. Wir definieren eine weitere Funktion vom Typ : diag :: (α stream)stream → (α list)stream mit = )) ( (:) : ] [ ) : ) : (( xs diag xs zipWith x xss xs x diag

Die Idee für eine Funktion die dieses erfüllt, verwendet eine Matrizendiagonali-sierung. Sie übernimmt einen stream of streams. Diesen kann man sich als eine infinite Matrix vorstellen welche eine unendliche Anzahl von Zeilen und Spalten hat. Diese Matrix wird nun diagonal abgearbeitet, so dass sich hieraus ein stream aus finiten Listen ergibt: 

x  00

x 

¹⁰ diag 

x

 20



Μ 

Wenn wir infinite Streams diagonalisieren können, warum haben wir das nicht gleich ganz am Anfang getan, als uns die Funktionen einfache lazy streams zurückgegeben haben? Definieren wir einmal den alten Kombinationsoperator mit Hilfe unserer neuen Funktion diag wie folgt: ⋅ ⋅ ⋅ = ∧ f g diag concat f g *

In Anlehnung an unser kleines Faktorisierungsprogramm wählen wir
∧ =

n test g Ergebnis aller Faktorkombinationen wieder. Für n=6 erhielten wir dann folgenden Stream, nachdem f und g* berechnet wurden: Λ ⊥ ⊥ ⊥ ⊥ ⊥ ⊥ ⊥ ⊥ ] , , , : ] 1 , 6 [ , , , : ] 2 , 3 [ , : ] 3 , 2 [ , : ] 6 , 1 [[

Wählt f eine Zahl die ein Faktor von n ist, hier 1, 2, 3, 6 dann gibt g einen Stream wieder der als erstes Element das korrekte Faktorenpaar hat, danach rechnet die Funktion mit 1 an erster stelle weiter terminiert aber nie. Wählt f eine Zahl die kein Faktor von n ist, so verfängt sich die Funktion sofort in einer nichtterminierenden Berechnung. Wenden wir nun diag auf diesen String an, so divergiert diese Funktion bereits nach dem ersten Element [1,6], denn es durchläuft ebenso den infiniten tail. Für [2,3] gibt es keine Möglichkeit mehr bei einer folgenden Berechnung den Index festzulegen, denn es gibt ja bereits nach [1,6] eine unendliche Anzahl von Entscheidungen, auch wenn sie alle eine leere Liste zurück geben. Das Matrizen-Modell muss also re-definiert werden, damit join die richtige Form bekommt. Mit unserer Hilfsfunktion diag können wir join nun wie folgt komponieren: ^⋅ α α α α     →   →    →  concat concat diag trans ^{)* ( *} LS LLLS LLSS LSLS

^. concat = concat ^. h** ⁶ zur Erinnerung: h*

Page 8

∧ durch die so definierte Funktion join festgelegt, Wird unser neuer Kombinationsoperator ' so muss sie auch assoziativ sein. Dies ist leider nicht so.

Jede finite Liste, welche durch h ∧ g ∧ f erzeugt wird, enthält alle Ergebnisse mit dem Gesamtindex x + y + z, wobei x, y und z angeben wie viele Auswahlen gebraucht wurden um f, g und h zu berechnen. 7

Die Ergebnismenge{(x,y,z)x + y + z =const} lässt sich als Dreieck in einem 3dimensionalen Raum darstellen:

4. Assoziativität von join

Das obige Problem existiert nur, solange wir es mit geordneten Listen zu tun haben. Wenn es uns egal ist, in welcher Reihenfolge uns die Ergebnisse, die den gleichen Index tragen, übergeben werden, so gilt h ∧ (g ∧ f) = (h ∧ g) ∧ f. Es geht letztendlich nur um das Dreieck als Ergebnisraum und nicht um seine Erschließung.

Diese Idee können wir dazu verwenden, für join die gewünschte Assoziativität herzustellen. Definition: Ein Bag ist eine endliche Liste in welcher die Reihenfolge der Elemente irrelevant ist. ⁸ (1) Wenn gilt f :: α → β dann ist f◊ :: α bag →β bag und union :: (α bag) bag → α bag

(2) Implementieren wir Bags über finite Listen so schreiben wir f*, in diesem Fall wird union über concat realisiert.

(3) Seien zwei Bags über finite Listen implementiert, dann sind die Bags gleich, wenn die eine Liste eine Permutation der anderen Liste ist.

Tauschen wir die zuvor verwendeten Listen gegen Bags aus so können wir für join Assoziativität nachweisen. Behauptung join ist assoziativ, es gilt: ⋅ = ⋅ join join join join ◊*

⁷ also den jeweiligen Index

⁸ Es können in Bags ebenfalls mehrere gleiche Elemente vorkommen.

Page 9

Vorbereitungen für den Beweis Allgemeine Gesetzmäßigkeiten: 1.) für ◊ und * gilt: ( g . f )* = g* . f* (g . f) ◊ = g◊ . f◊

2.) polymorphe Funktionen ⁹ wie diag sind natürliche Transformationen, so dass für jede Funktion f gilt: diag . f** = f◊* . diag

Page 10

Wir haben nun einige Hilfsfunktionen und ihre Beziehungen untereinander, sowie einige nützliche Definitionen zusammengetragen mit deren Hilfe wir die Assoziativität von join zeigen können. Ganz zu Anfang haben wir die Assoziativität für den herkömmlichen Kompositionsoperator ∧ gezeigt. Können wir die Assoziativität von join zeigen, so läßt sich ∧ anwenden. Wie zu Anfang schon der erste Beweis auch auf unseren neuen Operator ' einmal erwähnt wurde.

Beweis

In Abschnitt 2 definierten wir die gesuchte Funktion join wie folgt:

^⋅ α α α α     →   →    →  concat concat diag trans ^{)* ( *} LS LLS LLSS LSLS

Aus 1.) folgt für (concat . concat)*= concat* . concat*

Da wir hier auf Bags operieren müssen wir concat durch union vertauschen. So erhalten wir für join folgende Definition: ⋅ ⋅ ⋅ * * * :: trans diag union union join (Φ)

Für die Assoziativität von join erhalten wir dann:

Page 11

= ⋅ join join join join ◊*

 ^Φ union* . union* . diag . trans* . union* . union* . diag . trans* →

= union* . union* . diag . trans* . union*◊* . union*◊* . diag◊* . trans*◊*

Im vollständigen Beweis ist für jedes Diagramm angegeben warum es kommutiert. Dabei bedeutet A* die Verwendung von Lemma A, bei dem auf beiden Seiten der Funktor * hinzugefügt wurde und [union*] zeigt an, dass union* eine natürliche Transformation darstellt.

α(BS) 3

αB ² S ² BS

αB ³ SBS

αB ² SBS

α(BS) 2

Dies ist nur das äußere Gerüst des Beweises, zusätzlich müssen auch alle inneren Diagramme kommutieren. Aus Platzgründen wurden sie hier weggelassen. Wer den ganzen Beweis nachvollziehen möchte, der schaue hierzu in den referierten Text.

5. abschließende Betrachtung

∧ der hier für die Breitensuche entwickelt wurde, und Der assoziative Kompositionsoperator '

der sich in der logischen Programmierung wie ein ‚AND’ verhält, ist nur ein Teil einer größeren algebraischen Theorie, welche sich mit Suchstrategien in der logischen Programmierung auseinandersetzt.

Parallel zu diesem AND-Operator entwickelten Michael Spivey und Silvia Seres einen ∨ welcher sich wie folgt definieren lässt: entsprechenden OR-Operator '

Page 12

∨ g) x = zipWith(++)(fx)(gx) (f ' ∧ und ' ∨ weisen unter einer Reihe anderer algebraischer Die beiden Operatoren '

Eigenschaften auch Distributivität auf und es gibt ein neutrales Element für jeden Operator. Die neutralen Elemente dieser Operatoren sind die Funktionen true und false wobei: true :: α → α matrix definiert durch: ¹⁰ true x = repeat x : → neutrales Element für ' ∧

false:: α → β matrix definiert durch:

false x = repeat ∨ → neutrales Element für '

Infopapier

Verwendete Begriffe und Listen-Operationen:

xs
xss xsss ...

1. feststehende Operationen

concat

Diese Funktion konkateniert eine Liste von Listen in eine große Liste. Sie entspricht also der großen Vereinigungsmenge in der Mengenlehre ( ++ ist die kleine Vereinigung, da hier einfach zwei Listen gleichen Typs konkateniert werden ). Es gilt also: concat [[α]] → [α] ← ← ] ; xs x xss xs x concat xss = [

¹⁰ senkrechte Doppelstriche stehen für Bags

Page 13

Beispiel:

concat [[1,2],[a,b],[x,y,3]] = [1,2,a,b,x,y,3]

zipWith

Diese Funktion übernimmt ein Listenpaar und kombiniert jeweils das n-te Element der einen Liste mit dem n-ten Element der anderen Liste. Wenn die beiden Argumentenlisten nicht gleich lang sind, hat die Ergebnisliste die Länge des kürzeren Arguments.

Beispiel:

[1,2,3,4] zipWith([a,b,c]) = [(1,a), (2,b), (3,c)]

head

Diese Funktion wählt das erste Element einer Liste. head([x]++xs) = x Beispiel: head([h,e,a,d]) = h

tail

Diese Funktion wählt den Rest einer Liste ohne das erste Element. tail([x]++xs) = xs

Beispiel :

head([h,e,a,d]) = [e,a,d]

Die Beziehung zwischen head und tail kann folglich ausgedrückt werden über:

x = [head xs] ++ tail xs

foldr

Die meisten bisher genannten Operationen liefern Listen als Ergebnisse. Demgegenüber ist ein Faltungsoperator allgemeiner, weil er Listen auch in andere Werttypen umformen kann. Für das Falten nach rechts auf Listen gilt:

β α β χ β α → → → → → ] [ ) (

Bei faltr ist die Klammerung rechtsassoziierend, das heißt für die Anwendung auf eine Funktion über Listen: faltr fa[x 1 , x 2 , …,x n ] = fx 1 (fx 2 (…(fx n a)…)) wobei a das neutrale Element ist.

Das zweite Argument der Funktion muss den gleichen Typ besitzen wie das Ergebnis der Funktion, während das erste Argument im allgemeinen einen anderen Typ besitzen kann.

Sei ⊕ eine Operatorvariable, die an eine Funktion mit zwei Argumenten gebunden ist, dann kann wie folgt rechts gefaltet werden:

faltr(⊕) a [] = a

faltr(⊕) a [x 1 ] = x 1 ⊕ a faltr(⊕) a [x 1 , x 2 ] = x 1 ⊕ (x 2 ⊕ a ) faltr(⊕) a [x 1 , x 2 , x 3 ] = x 1 ⊕ (x 2 ⊕ (x 3 ⊕ a ) ) … Beispiele: summe = faltr (+) 0 produkt = faltr (*) 1 concat = faltr (++) [] 2. generierte Operationen

Page 14

choose

Diese Funktion wird im Beispiel der Faktorensuche für eine gegebene Zahl n zur Auswahl der einzelnen Faktoren verwendet. Sie tritt in zwei Variationen auf: (1) choose = [xs++[x] x ← [1…]]

(2) choose = [[xs++[x]] x ← [1…]]

test

Diese Funktion übernimmt ein Paar ausgewählter Faktoren und überprüft, ob sie Faktoren der vorgegebenen Zahl n sind. Falls dies der Fall ist wird das Paar in einen Stream of Lists geschrieben, ansonsten wird eine leere Liste geschrieben. Auch hier gibt es zwei Variationen:

(1) test n[x,y] = if x . y = n then [[x,y]] else [] (2) test n[x,y] = if x . y = n then [[[x,y]]] else []

factorize

Diese Funktion setzt die Funktionen choose und test so zusammen, dass nach Faktorenpaaren für eine Zahl n gesucht werden kann. ( Die Ausführung geschieht von rechts nach links ).

∧ ∧ )[] ( choose choose n test (1) factorize n =

∧′ ∧′ = )[] ( choose choose n test n factorize (2)

trans

Diese Funktion vertauscht zwei Werttypen und ist vergleichbar mit einem fold auf Listen. Sie wird hier dazu verwendet eine Liste aus Streams in einen Stream aus Listen umzuschreiben.

trans[] = repeat []

trans(xs:xss) = foldr (zipWith(:))(repeat[])

Diese Funktion nimmt also eine Liste in der streams enthalten sind. Von jedem stream nimmt sie das erste Element (head) und schreibt alle ersten Elemente in eine Liste (nach Reisverschlussprinzip), danach wird das ganze mit dem zweiten und jedem weiteren Element wiederholt, da wir zu Anfang eine Liste aus Strings haben, erzeugen wir auf diese Weise eine divergierende Liste aus finiten Listen: einen stream of lists. Das heißt, wir können trans alternativ auch wie folgt definieren: trans xss = (head*xss):(trans(tail*xss))

diag

Diese Funktion nimmt einen Stream aus Streams und verwandelt ihn in einen Stream aus finiten Listen. Dies geschieht indem eine infinite Matrix diagonalisiert wird:

 x

 00

x 

¹⁰ diag 

x

 20



Μ 

Diese Funktion sieht folgender maßen aus: = xs diag xs zipWith x xss xs x diag )) ( (:) : ] [ ) : ) : ((

Page 15

3. Verwendete Werttypen

list

Hierbei handelt es sich um eine gewöhnliche Liste von Elementen deren Position festgelegt ist. In einer Liste treten alle Elemente nur einmal auf. stream

..ist seinem Wesen nach auch nichts anderes als eine Liste. Das besondere ist aber die Art und Weise wie diese Liste verarbeitet wird. Da ein Stream potentiell infinit ist, würde es keinen Sinn machen vor seiner Weiterverarbeitung darauf zu bestehen, dass alle enthaltenen Elemente bereits fest definiert sind. Daher wird ein stream mittels ‚lazy evaluation’ ausgewertet. Das bedeutet, jedes Element wird nur dann konkretisiert, wenn es tatsächlich gebraucht wird und dann auch nur ein einziges mal. matrix

Der Werttyp matrix beschreibt einen Stream aus Listen. Der Idee nach, werden alle Listen untereinander geschrieben, so dass eine Matrix entsteht, deren Zeilen an sich zwar endlich sind, deren Zeilen Anzahl aber infinit sind. bag

Ein Bag ist eine spezielle Art von Liste. Anders als bei herkömmlichen Listen ist die Reihenfolge in einem Bag nicht festgelegt, d.h. es gibt weder ein erstes noch zweites noch n-tes Element. Außerdem kann ein Bag ein Element mehrmals aufnehmen. Bags können auch über finite Listen realisiert werden. Ist dies der Fall, dann gilt für zwei dieser Bags Gleichheit, wenn die eine finite Liste eine Permutation der anderen Liste ist, da ja die Reihenfolge irrelevant ist.