Fibonacci-Zahlen

Page 1

Röntgen-Gymnasium Kollegstufen-Jahrgang 00/02

Thema: Fibonacci-Zahlen

Verfasser: Michael Mützel

Leistungskurs: M7 Kursleiter: StD Serger Abgabetermin beim Kursleiter: 01.02.2002

Page 3

In dem Liber Abaci gibt Fibonacci sein Wissen über Arithmetik und Algebra wieder. Es enthält sinngemäß auch folgende Übungsaufgabe zur Addition, die zu der berühmten Fibonacci-Reihe führt (vgl. Nr.2):

Das Hasenproblem: Zu Beginn eines Jahres gibt es in einem umzäunten Garten genau ein neugeborenes Hasenpaar. Jedes Hasenpaar erzeugt während seines Lebens jeden Monat ein weiteres Paar. Ein neugeborenes Paar wird nach einem Monat fruchtbar und bekommt somit nach zwei Monaten seine ersten Nachkommen. Es soll angenommen werden, dass die Hasen nie sterben. Wie viele Hasenpaare sind nach einem Jahr in diesem Garten?

Im Monat 0 gibt es 0 Hasenpaare. Im Monat 1 wird ein neugeborenes Paar in den Garten gesetzt. Im Monat 2 lebt dieses eine Paar immer noch, es konnte sich aber noch nicht fortpflanzen, da es erst nach einem Monat geschlechtsreif wird; die Zahl der Paare im Monat 2 ist immer noch 1. Im Monat 3 leben alle Paare aus Monat 2 zusätzlich den Neugeborenen. Die Zahl der Neugeborenen entspricht der Zahl der Paare zwei Monate zuvor, also im Monat 1, da die damals Lebenden jetzt mindestens zwei Monate alt, also fortpflanzungsfähig, sind. Damit leben im Monat 3 genau 1+1=2 Hasenpaare. Im Monat 4 sind es 2+1=3 Hasenpaare, im Monat 5 sind es 3+2=5 usw.

Page 4

F , addiert mit der Anzahl der Paare im zwei Monate früher gelegenen Vormonat,

− 1 n

Monat, F :

− 2 n

Somit hat das Hasenproblem zu einer rekursiv definierten Folge geführt, die als Fibonacci-Reihe, bekannt wurde.

Die folgende Tabelle zeigt den Beginn der Fibonacci-Folge:

Die Lösung des Hasenproblems ist also 13 F =233, denn zu Beginn des 13. Monats ist genau ein Jahr verlaufen.

Obwohl die Fibonacci-Reihe ursprünglich nur zur Lösung des Hasenproblems diente, besitzt sie diverse interessante Eigenschaften, welche sie einer näheren Betrachtung würdig machen. Leider werden die Fibonacci-Zahlen im Unterricht nicht behandelt, weshalb ich sie in dieser Facharbeit vorstellen möchte. Eine der bekanntesten Eigenschaften der Reihe ist ihr Zusammenhang mit dem Goldenen Schnitt. Der Quotient zweier benachbarter Zahlen F , der Fibonacci- − n 1

Reihe ergibt bei steigendem n verblüffend genau das Teilverhältnis wieder, das in der antiken Architektur als besonders ästhetisch empfunden wurde und auch in der Natur häufig anzutreffen ist. Außerdem besitzt die Reihe einige Summations- und Teilbarkeitsregeln, bei deren Herleitung sich gut das wichtige Induktionsverfahren üben lässt. Diesen Eigenschaften werden sich die folgenden Kapitel dieser Arbeit zuwenden. Die Fibonacci-Reihe findet auch in anderen Wissenschaften Anwendung, etwa in der Biologie und der Physik, doch da dies eine Facharbeit im Fach Mathematik ist, werde ich hierauf nicht näher eingehen.

Page 5

gilt, dann teilt der Punkt S die Strecke AB im Goldenen Schnitt. Man nennt dies auch stetige Teilung.

Der Goldene Schnitt erhielt diesen Namen, weil dieses Teilverhältnis den Menschen besonders ästhetisch erscheint. Er ist heute in der Architektur, der Malerei, der plastischen Kunst und vielen anderen Bereichen zu finden. Als Beispiel dient die folgende Skizze eines antiken griechischen Tempels. Im Verhältnis der stetigen Teilung stehen jeweils die Höhe und Breite des Gebäudes sowie die Gebäudehöhe und die Säulenlänge zueinander.

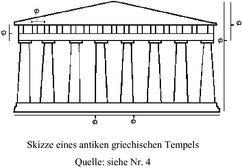
Allerdings ist der Goldene Schnitt keine Erfindung eines Menschen, sondern er kommt auch in der Natur häufig mehr oder weniger deutlich vor, z.B. bei den menschlichen Gliedmaßen. Bei genauerem Interesse vergleiche man hierzu auch Quelle Nr. 5.

Page 6

fällt ein Lot auf AB in B, trägt ½ AB an, um den Punkt C zu erhalten. Um C wird ein

Kreis mit Radius BC gezeichnet, der Schnittpunkt des Kreises mit AC heißt D. Zuletzt konstruiert man einen Kreis um A mit Radius AD , der die AB in S schneidet. Der Punkt S teilt die Strecke AB im Goldenen Schnitt, d.h. = SB AS AS AB :

Der Beweis für die Richtigkeit dieser Konstruktion ist im Anhang nachzulesen. = AS = setzt, lässt sich das Teilverhältnis auch so Wenn man die Länge 1 AB und x schreiben:

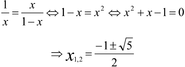
und da x positiv sein muss

Das bedeutet, der Goldene Schnitt teilt Strecken etwa im Verhältnis 1

Interessant ist nun der Vergleich mit dem Quotienten

nächsten Seite zeigt. Bei steigendem n nähert er sich dem Verhältnis des Goldenen Schnittes scheinbar zunehmend genauer an. Der relative Fehler, der sich als

berechnen lässt, liegt schon bei 7 F nur noch im Promille-Bereich, für n=21 beträgt er sogar nur noch wenige Milliardstel (vgl. Tabelle Seite 7).

Page 7

Die Tabelle legt die Vermutung nahe:

Der Beweis kann aber an dieser Stelle noch nicht erbracht werden. Er erfolgt jedoch im weiteren Verlauf dieser Facharbeit im Kapitel Anhang: Nachtrag zum Goldenen Schnitt.

Page 8

Die Addition zweier beliebiger Fibonacci-Zahlen n F , ergibt nicht sicher wieder eine

m

Fibonacci-Zahl, wie folgendes Beispiel zeigt: = + = + F 4 3 1 F

4 2

Ein Blick in die Tabelle auf Seite 4 zeigt, dass 4 nicht zu der Reihe gehört. Nun werden weitere Summationen von Gliedern der Fibonacci-Reihe durchgeführt. Zuerst sollen alle Glieder von 1 F bis n F fortlaufend addiert werden. Die einzelnen

Glieder lassen sich durch einfache Umformung aus der obigen Gleichung (3) so − = darstellen: F

2 3 1

+ − = F

+ 1 2 n

Jetzt addiert man all diese Gleichungen miteinander. Da auf der rechten Seite jeder Summand außer 2 F und F einmal positiv und einmal negativ vorkommt, erhält man:

+ 2 n

Auf ähnliche Weise kann man auch die Summe der ersten n ungeraden Fibonacci- F = Zahlen berechnen: F

2 1

− =

Page 9

Analog verläuft auch die Herleitung der Summe der ersten n geraden Fibonacci-Zahlen, weshalb ich sogleich das Ergebnis angebe:

Bei den obigen Beispielen wurden jeweils verschiedene Glieder der Fibonacci-Reihe miteinander addiert. Im Anschluss wird auch die zweite Grundrechenart, die Multiplikation, eingeführt.

Wir beginnen mit folgendem Satz, der noch zur Herleitung einer weiteren Summe und der Teilbarkeitsregeln benötigt wird: + = F (4)

+ − + 1 m n m n m n

Bewiesen wird dieser Satz mit Hilfe der vollständigen Induktion. Hierzu wird vorerst das Prinzip der Induktionsbeweise gezeigt: Für jedes ∈ n N sei eine Aussage A(n) erklärt, die wahr aber auch falsch sein kann. Wenn folgende Vorraussetzungen erfüllt sind (I.) A(0) ist wahr

(II.) Wenn die Aussage A(n) wahr ist, soll stets die Gültigkeit von A(n+1) folgen, dann ist A(n) wahr für alle ∈ n N.

Die Induktionstechnik wird zunächst an einem einfachen Beispiel verdeutlicht. Zu beweisen ist:

Zum Beweis: Induktionsbeginn: n=1

+ ⇒ n Induktionsschluss: 1 n Es sei schon gezeigt: +

∑ = ν

2

= ν 1

Dann

Page 10

Nach dieser kurzen Einführung in das Induktionsverfahren kehren wir zum Beweis von Satz (4) zurück. Hier erfolgt der Induktionsschluss leicht verändert. Statt + ⇒ n wird hier + ⇒ + 2 1 , n

gefolgert. Deshalb wird auch der Induktionsbeginn erweitert: + = ⇔ + = ⇒ m=1 F (vgl.(2))

− + − + n 1

+ = ⇒ + = ⇔ + = ⇔ m=1+1 F F 2

+ − + − + − + 1 2 1 2 n n 1 2 1 2

+ = ⇔ F (vgl.(3))

+ n 1 2

Induktionsschluss: + = F

+ − + 1 m n m n m n

+ = F

+ − + 2 1 m n m n m n

Durch Addition der letzten beiden Gleichungen ergibt sich:

was zu beweisen war.

+ = ⇒ F (4)

+ − + 1 m n m n m n

ist für jedes beliebige natürliche m, n gültig.

Diesen Satz kann man bei dem Beweis folgender interessanten Eigenschaft der Fibonacci-Reihe gut verwenden: Die Quadrate zweier benachbarter Fibonacci-Zahlen ergeben addiert immer eine weitere Fibonacci-Zahl; + = + ² F (5)

+ 1 2 1 n

Der Beweis erfolgt wieder durch das oben beschriebene Induktionsverfahren. = + = + ² Als Beispiel: 1 ² 1 ² 0 F

+ 1 0 1 0

+ = + ⇒ ² F

+ 1 2 1 k

( ) ( ) ² = + = + = + ² 2 F

+ − + − + 1 2 1 k

= + = ² 2 ) ( 2 ) ( F

+ − k 1

= + = mit (5): 2 F

+ − + − k 1 2 1 2

= + + = + = + = mit (4): 2 F F

+ − + − + k 1 2 1 2 1 2 1 2 2 1 2 k = k

Page 11

Auch der folgende Satz lässt sich durch Induktion beweisen: ( ) n − = − ² F 1

+ − 1 n

( ) ¹ − = − ⋅ ⇔ − = − ² 1 0 1 F stimmt für n=1:

+ − 1

Im Folgenden wird bewiesen, dass die Gleichung auch für n=k+1 richtig ist, wenn sie ( ) k − = − ² für n=k stimmt: F 1

+ − k 1

( ) k − = − ⇔ ² F 1 ) (

+ k 1

( ) k ² − = − ⇔ ² F 1

+ k 1

( ) k ² − = + − ⇔ F 1 ) ( 1

+ k 1

( ) k

Page 12

In diesem Kapitel soll die Teilbarkeit innerhalb der Fibonacci-Reihe untersucht werden. Ein Blick auf die ersten Glieder der Reihe, siehe Tabelle auf Seite 4, zeigt, dass zwei benachbarte Fibonacci-Zahlen dort immer teilerfremd sind, d.h. der größte gemeinsame Teiler, kurz ggT, ist die Zahl 1. Es wird nun bewiesen, dass diese Eigenschaft auch für die gesamte Reihe gültig ist.

Der Beweis gelingt durch das Aufzeigen eines Widerspruchs. Man nimmt an, es gäbe zwei benachbarte Zahlen , + n F , für die gilt:

1 n

= t F ggT + ) , F (

n 1 n

> , ∈ mit 1 t t N Also kann man , + n F auch als Produkte aus t und den natürlichen Zahlen , + n t

1 n 1 n

⋅ = ⋅ = + formulieren: t F und t F

+ n n 1

Mit (2) folgt: − ⋅ = − = ) ( 1 t F

+ − 1 n

− = + Dabei ist t wieder eine natürliche Zahl. Daraus folgt, dass auch

− n 1

F mit n F den Teiler t gemeinsam hat. Durch analoges Fortfahren ergibt sich, dass t

− 1 n

1 = > auch Teiler von ,..., F ist. Da aber 1 F nicht durch 1 t teilbar ist, ist die

− 1 3 2 n

Annahme falsch.

⇒ Zwei benachbarte Fibonacci-Zahlen sind teilerfremd.

Ein weiterer Satz über die Fibonacci-Reihe besagt:

Wenn m Teiler von n ist, dann ist auch m F Teiler von n F :

m ⇒ m F n

n

Man kann diesen Satz leicht durch Induktion beweisen. Induktionsanfang: ⋅ = , mit ∈ m k n k N

Für k=1 trifft der Satz sicher zu, da m F .

m , mit ∈ ⋅ = ⇔ ⇒ Induktionsschluss: F l F l N

⋅ m km

= F )

^{+ ⋅ +} m km k 1 (

( ) m ⋅ + = ⋅ + = + = mit (4): F l F l F

+ − + − + − m km km km km 1

⇒ m F q.d.e.

Page 13

Die Fibonacci-Reihe ist eine rekursiv definierte Zahlenfolge. Um g F zu berechnen,

müssen wir bislang jedes einzelne Glied, das sich zwischen g F und den beiden Zahlen

− + = F , befindet, über die Gleichung F bestimmen. Dabei sind

− − m 1 2 1 n

F , die beiden g F am nächsten liegenden bekannten Zahlen. Wenn aber

− m 1

beispielsweise g sehr groß ist und nur 0 , F gegeben sind, stellt die Berechnung von

1

F auf diese Weise einen großen Aufwand dar, weil g-m Rechenschritte ausgeführt

g

werden müssen. Es stellt sich daher die Frage, ob man eine Fibonacci-Zahl nicht direkt in Abhängigkeit ihres Indexes berechnen kann, ohne ihre Nachbarn dafür kennen zu müssen.

Zu diesem Zweck wird eine andere Folge mit der Eigenschaft − + = Z (6)

− 2 1 n

gesucht, bei der man das n-te Glied direkt ausrechnen kann. Ein Kandidat für eine ^{3 2 1} ,... , 1 solche Folge ist die Reihe z

Nun muss z so gewählt werden, dass die Gleichung ⁻ + = 2 1 n z − 2 n erfüllt wird. Wenn man die Gleichung durch z dividiert, erhält man: + = z ² 1 z

Die Lösungen dieser Gleichung lauten

′ ′ = = n n Folglich erfüllen die beiden Reihen z Z und z Z die Bedingung (6).

n 1 n 2

Man kann diese zwei Gleichungen mit den Parametern a und b multiplizieren und anschließend addieren: ′ + = + Z b Z b Z a Z a Z b Z a

− 2 1 2 n

′ ⇔ + = + ) ( ) ( Z a Z b Z b Z a Z b Z a

− 2 1 n

Also ist auch ′ = + Z b Z a (7)

n

eine rekursiv definierte Folge, welche die Eigenschaft (6) besitzt. Sie wird durch ihre Z ′ die Fibonacci-Zahlen ersten beiden Glieder vollständig festgelegt. Da wir über n berechnen wollen, muss gelten:

Page 14

′ ′ F und Z F

0 1

′ ⇔ 1 0 Z b Z a Z b Z a

1 0

+ = ∧ + = ⇔ ^{1 0} 1 0 bz az bz az

2 1 2 1

+ = ∧ ⋅ + ⋅ = ⇔ 1 0 bz az b a

2 1

⇔

Nun müssen die so erhaltenen Werte für die Parameter a und b in (7) eingesetzt werden, um die Fibonacci-Zahlen direkt berechnen zu können.

Diese Formel wurde 1843 von Jacques P.M. Binet entdeckt (vgl.Nr.7).

Page 15

Nachdem die Formel von Binet bekannt ist, kann bewiesen werden, dass der Grenzwert des Quotienten zweier benachbarter Fibonacci-Zahlen für unendlich große n tatsächlich dem Verhältnis des Goldenen Schnittes entspricht. Behauptung:

Beweis:

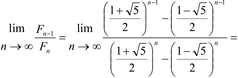
wegen

Zuletzt soll bewiesen werden, dass der Punkt S nach der auf Seite 6 angegebenen Konstruktionsmethode die Strecke AB stetig teilt:

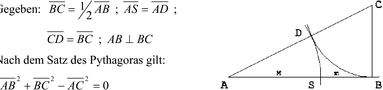
Gegeben:

Nach dem Satz des Pythagoras gilt:

) ( ) ( ) 0 (

^{2 2 2} 1 = + − + ⇔ = ⋅ − + ⋅ ⇔ AS AB AB SB AS 0 2 AS AB SB SB AS

2 − + SB AB SB AS AB SB ² ⋅ − ⋅ = + ⋅ ⇔ = ⇔ − = + ⇔ SB AS AS AB SB SB AS 1

SB ASB AS AS AB =

⇔ q.e.d.

SB AS

Page 16

1) Meschkowski, H.: Mathematiker-Lexikon, Hochschultaschenbücher-Verlag, Mannheim 1964

2) Mathematik-Online, Internetadresse: http://www.mathematik-online.de/F9.htm, aufgerufen am 16.01.02

3) Dr. Wolff, G.: Handbuch der Schulmathematik, Band 3, Geometrie der Unter- und Mittelstufe, Hermann Schroedel Verlag KG, Hannover, Verlag Ferdinand Schöningh, Paderborn, o.O. 1967²

4) Schönfeld, M.: Facharbeit der Mathematik, Leonardo Fibonacci, Internetadresse: http://langheim.net/take1.htm, aufgerufen am 24.12.01 5) Internetadresse: http://www.asamnet.de/~hollwecm/section/anwendung3.htm, aufgerufen am 24.01.01

6) Internetadresse: http://www.uni-jena.de/~x8moma/grundl.htm, aufgerufen am 24.12.01 7) Massin, H.: Mathe-Kiste, Internetadresse: http://www.mathekiste.de/fibonacci/kanin.htm, aufgerufen am 16.01.02

Ich erkläre hiermit, dass ich die Facharbeit ohne fremde Hilfe angefertigt und nur die im Literaturverzeichnis angeführten Quellen und Hilfsmittel benützt habe.

.........................., den................

..................................................