Value at Risk: Konzept und Anwendungsmöglichkeiten

^{Value at Risk: Konzept und Anwendungsmöglichkeiten}

wirksamen Risikoquantifizierung und Messung wurde immer lauter. Außerdem ist es von enormer Bedeutung, welche Rendite mit welchem Risiko erwirtschaftet werden kann. ² Der Value at Risk (VaR) wird als Instrument der Risikoquantifizierung am häufigsten genannt. Alternative Bezeichnungen sind capital-at-risk und money-at-risk. Der VaR ist ein einseitiges verlustorientiertes Risikomaß und unterscheidet sich dadurch von Streuungsmaßen (z. B. Standardabweichung), welche ein beidseitiges Schwankungsrisiko messen. Beim VaR werden die Verluste quantifiziert, es wird aber keine Gegenüberstellung mit den erwarteten Gewinnen durchgeführt. ³

^{In der vorliegenden Arbeit wird zuerst der Prozess des Risikomanagement in den Grundzügen erläutert. Anschließend werden in Kapitel 3 die nötigen Grundlagen erarbeitet, die im Kapitel}

während des gesamten Risikomanagementprozess Rechnung getragen werden. Der Risikomanagementprozess untergliedert sich in drei Phasen: - Risikoidentifikation

- Risikoquantifizierung

- Risikosteuerung

2.1 Risikoidentifikation Die Aufgabe der Identifikation von Risiken liegt darin, mögliche Gefährdungspotentiale im Unternehmen zu lokalisieren. ⁵ Außerdem ist es wichtig festzulegen, welche Unternehmensrisiken erfasst werden sollen. Die Risiken lassen sich in allgemeine externe Risiken (z.B. Abhängigkeit von Fördermitteln), leistungswirtschaftliche Risiken (z.B. häufige Terminverschiebung von Aufträgen), finanzwirtschaftliche Risiken (z.B. sind noch Finanzierungsspielräume vorhanden) und Risiken aus Corporate Governance (z.B. sind die Leistungsträger im Unternehmen Einzelkämpfer oder existiert eine Teamkultur) einteilen. ⁶ Eine methodengestützte Möglichkeit die Risiken zu identifizieren ist der „Top-down“ Ansatz. Zuerst werden auf Vorstandsebene bestandsgefährdende Risiken diskutiert. Danach betrachtet man die Bereiche, in denen die Risiken auftreten können genauer. Im letzten Schritt werden die Bereiche und Prozesse untersucht, auf die zuvor nicht näher eingegangen wurde. Ein nicht methodengestütztes Konzept zur Risikoidentifikation ist die Form des offenen Brainstormings. Der Vorteil ist, das hier auch ein Augenmerk auf Kleinstrisiken gerichtet wird. ⁷

Sensitivitätsanalysen sowie der Value at Risk diskutiert.

Um das Risiko mit der Standardabweichung zu berechnen gibt es zwei Möglichkeiten. Erstens kann aus den historischen Werten die Standardabweichung geschätzt werden. Zweitens ist es möglich unter der Annahme einer Verteilung der Renditen die Standardabweichung zu berechnen. Die erste Möglichkeit ist obwohl man eine empirische Datenbasis benötigt, der zweiten vorzuziehen, da sie nicht auf einer subjektiv geschätzten Verteilungsannahme beruht. ⁹

Beispiel:

Aus den täglichen Renditen des CHF und des USD gegenüber der DM in der Zeit vom 01.01.95 bis zum 31.03.95 können folgende Erwartungswerte und Standardabweichungen geschätzt werden.

) = -0,0387%,

) ) ) µ σ = µ σ = % 2260 , 0 ; = -0,1794%, % 7807 , 0

CHF CHF USD USD

(Jeweils pro Tag)

Ist nur die Standardabweichung der Renditen das Risikomaß, so folgt, dass das Risiko des CHF geringer ist als das des USD.

Vermögensposition, der mit einer Wahrscheinlichkeit von (1-α) während eines definierten Zeitraums nicht überschritten wird. (siehe Abbildung 1) 10

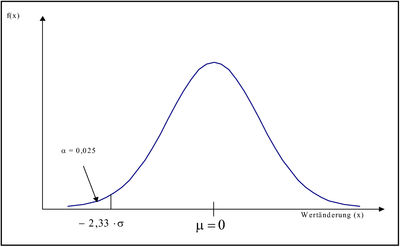
^{A b bild un g 1: D ichte fun ktion e iner N o rm a lverteilun g u nd V A R}

Beispiel:

Ein Investor hält am 31.03.95 eine Position von 100 Millionen CHF (Gegenwert 123,33 Mio. DM). In den letzten drei Monaten hatten die täglichen Erträge aus dieser Position einen Mittelwert von 46.093,75 DM und eine Standardabweichung von 268.697,96 DM. Der VaR zu einer Wahrscheinlichkeit von 99 % kann nun über das 1% Quantil bestimmt werden. σ µ ⋅ − − = ) ( z VaR

^{α ∆ − ∆ 1} V v

Der VaR beträgt: -(46.093,75 - 2,33 · 268.697,96) = 579.972,50 DM ¹¹ Ein Verlust von 579.972,50 DM wird also innerhalb eines Tages nicht überschritten. Dieser Wert entspricht in Abbildung 1 genau dem Punkt „-2,33 · σ“.

Für die erörterten Risiken müssen in einem nächsten Schritt nun geeignete Maßnahmen eingeleitet werden. Dies sind im einzelnen die Risikovermeidung, Risikominderung, Risikobegrenzung und die Risikokompensation. Unter Risikovermeidung versteht man, dass das Unternehmen vollständig auf die Vermögensposition verzichtet. Bei der Risikoverminderung soll die Wahrscheinlichkeit eines Vermögensverlustes verringert werden. Die Risikobegrenzung kann z.B. mit einer Stop Loss-Order durchgeführt werden. Bei der Risikokompensation geht das Unternehmen ein gegenläufiges Geschäft ein. Welche Maßnahmen die Entscheidungsträ- ger im einzelnen ergreifen, muss fallspezifisch ermittelt werden. ¹³ Der Value at Risk lässt sich als Instrument der Risikoquantifizierung interpretieren. Dadurch bildet er die Grundlage für die Risikosteuerung.

3. Grundlagen der Value at Risk Berechnung Bei der Bestimmung des Value at Risk ist es zuerst notwendig, einige grundlegende Schritte durchzuführen, bevor man ihn mit einem geeigneten Verfahren bestimmt. In diesem Kapitel werden die Grundfragen der Bestimmung des Portfolios, der Marktparameter, des Simulationshorizontes und des Konfidenzintervalls erörtert.

3.2 Bestimmung der Marktparameter Die Marktparameter (ξ) können am Markt beobachtet werden und haben einen Einfluss auf den Wert des betrachteten Portfolios. Marktparameter können z.B. Wechselkurse, Zinsen, Aktienkurse und Aktienindizes sein. Der Wert einer Dollaranleihe hängt beispielsweise von dem aktuellen Zinssatz und dem Wechselkurs ab. Nach der Identifikation muss die Wertentwicklung des Portfolios (PV) in Abhängigkeit von den Marktparametern quantifiziert werden ¹⁵ PV(ζ ¹ ,ζ ² ,...,ζ ^{N ).}

Außerdem müssen die Wechselwirkungen etwa mit Hilfe einer Kovarianzmatrix zwischen den Marktparametern beschrieben werden. Damit können risikominimierende Diversifikationseffekte zwischen den Risikofaktoren berücksichtigt werden. ¹⁶

horizonts und des Konfidenzintervalls. Einbeziehung von Worst-Case-Szenarien implizieren ein großes Konfidenzniveau. Oft werden dann nur mögliche extreme Ereignisse wie der Börsencrash von 1987 betrachtet. Der Simulationshorizont ist die Zeitspanne von der Risikoidentifikation bis zur Glattstellung der Position. ¹⁷ Daraus folgt, dass die Länge des Simulationshorizontes von der Liquidität des Marktes abhängt. Für Handelsaktivitäten werden deshalb oft Horizonte von einem Tag verwendet. Außerdem hängt der Simulationshorizont von der Länge des Planungszeitraums des Entscheidungsträgers ab. ¹⁸

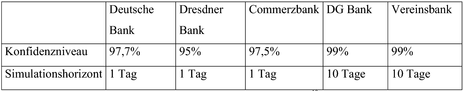
Tabelle 1: Konfidenzniveau und Simulationshorizont deutscher Großbanken ¹⁹

Die Zahlenwerte zeigen die Interdependenzen zwischen Konfidenzniveau und Simulationsho- auf. Je länger der Simulationshorizont ist, desto größer ist die Wahrscheinlichkeit auftretender Verluste. Deshalb lässt sich erklären, dass Banken mit langem Simulationshorizont tendenziell ein größeres Konfidenzintervall wählen (siehe Tabelle 1).

4. Berechnung des Value at Risk Nachdem die Risiken im Unternehmen identifiziert sind, kommt man im Prozess des Risikomanagements zur Risikoquantifizierung. Als ein Instrument wurde unter 2.2 der Value at Risk genannt. In der Literatur werden zur Berechnung des VaR der Korrelationsansatz (4.1), die Historische Simulation (4.2) und die Monte-Carlo-Simulation (4.3) eingehend diskutiert.

Der Korrelationsansatz 20 4.1

Der VaR kann berechnet werden, in dem man die Wertänderung des Portfolios, die Rendite oder die Marktparameter als Modellvariable zur Modellierung verwendet. In der Praxis wird für die Modellierung meist die Normalverteilung unterstellt, deshalb wird in diesem Kapitel nur auf diese eingegangen. Andere Verteilungen werden in der Schlussbetrachtung kurz besprochen.

Die Verwendung der Wertänderung der Modellvariable ist am wenigsten geeignet, da es sehr problematisch ist, diese als normalverteilt zu unterstellen. Man kann den VaR wie unter 2.2 σ µ ⋅ − − = ) ( z VaR mit der Formel [ ] bestimmen.

^{α ∆ − ∆ 1} V v

Aus der historischen Datenbasis werden die Parameter (Mittelwertvektor der Renditen M ,

r PF

Kovarianzmatrix ∑ PF r ) der multivariaten Normalverteilung der Renditen bestimmt. ^{21 Es}

empfiehlt sich die Darstellung in Matrizen.

µ  

Λ σ σ σ   r  

¹   r r r r r r ^{, ,} µ N ^{1 2 1 1 , 1}  

σ σ σ Λ r   = M ²   ∑ r r r r r r ^{, , ,} = r Μ N ^{2 2 2 1 2} ;   PF   Μ Ο Μ Μ r PF     µ

    r Λ σ σ σ

N  

r r r r r r ^{, , ,} N N N N ^{2 1}

kann a.) ∑ V (d.h. Short- und Longpositionen können sich ausgleichen) oder b.) ∑

V als

n n

n n

Basis verwendet werden. Die zweite Möglichkeit hat den Vorteil, dass der Term nicht Null betragen kann, wenn sich die langen und die kurzen Positionen ausgleichen. V mit ∑ = , = = n v 1 a.) N n v ,..., 2 , 1

∑ n n V

n n

V ∑ = l 1 , = = n b.) N n l ,..., 2 , 1 mit n ∑ n V n

n

v = l = T T Der Vektor ) ,...., , ( v v v bzw. ) ,...., , ( ² l l l wird als Anteilsvektor bezeichnet.

^{2 1} N ¹ N

r = T Wenn ) ,..., ( ² r r der Vektor der Renditen der einzelnen Vermögensgegenstände ist, so

N

⋅ = T berechnet sich die Portfoliorendite PF r durch r v r . Sie ist normalverteilt und wird

PF

µ v ⋅ = T durch die Parameter M ; beschrieben. Für die absoluten Werte ∑ ^⋅ T ^{σ ⋅ =} v v

r r r r PF PF PF PF

∑ ⋅ l ⋅ = µ T T σ ⋅ = ergeben sich die Formeln: M . ; l l

r r r r PF PF PF PF

Für ein Portfolio mit zwei Vermögensgegenständen ergeben sich folgende Vereinfachungen für die Parameter (für l ist die Formel identisch.):

µ µ µ ρ σ σ σ σ σ ⋅ + ⋅ = ⋅ ⋅ ⋅ ⋅ ⋅ + ⋅ + ⋅ = ^{2 2 2 2} v v 2 v v v v .

^{2 1 2 1} r r r r r r r ^{2 1} r r r ^{2 1 2 1 2 1 2 1} PF PF

Das Quantil der Verteilung der Renditen kann wie folgt berechnet werden: µ σ − ⋅ = ⁻ z r .

^α r r VaR 1

PF PF

In Abhängigkeit davon, ob man VAR r mit v oder mit l berechnet hat, ergibt sich der Value at ⋅ = Risk als: oder , PF r V VaR

VAR

= ∑ ⋅ n r V VaR

VaR

n

Nachfolgend wird an einem Zahlenbeispiel zuerst der Fall mit zwei und danach mit mehreren Vermögensgegenständen aufgezeigt.

wird für den gleichen Zeitraum ein Mittelwert von -0,1794% und eine Standardabweichung ρ − = von 0,7802% ermittelt. Die Renditen haben eine Korrelation von 5845 , 0 .

^{1 ,} r r 2

1.Berechnung mit Anteilsvektor v : V ^PF = 121,33 Mio. DM + (-69,19 Mio. DM) = 52,14 Mio. DM, − 19 , 69 33 . 121

− = = = 33 , 1 ; 33 , 2 v v

^{= 2 1} 14 , 52 14 , 52 µ µ µ = − ⋅ − + ⋅ = ⋅ + ⋅ = % 3281 , 0 %) 1794 , 0 ( ) 33 , 1 ( % 0387 , 0 33 , 2 v v

^{2 1} r r r ^{2 1} PF

ρ σ σ σ σ σ ⋅ ⋅ ⋅ ⋅ ⋅ + ⋅ + ⋅ = ^{2 2 2 2} 2 = v v v v

^{2 1 2 1} r r r r r r r ^{2 1 2 1 2 1} PF − ⋅ ⋅ ⋅ − ⋅ ⋅ + ⋅ − + ⋅ ⋅ ^{2 2 2 2} ) 5845 , 0 ( % 7807 , 0 % 226 , 0 ) 33 , 1 ( 33 , 2 2 % 7807 , 0 ) 33 , 1 ( % 226 , 0 33 , 2 =1,4093%

Das Renditequantil bei einem Wahrscheinlichkeitsniveau von 97,5% ergibt sich als.: µ σ = − ⋅ = − ⋅ = ⁻ % 4341 , 2 % 3281 , 0 % 4093 , 1 96 , 1 z r

^{α 1} r r VaR

PF PF

= 52,15 Mio. DM · 2,4341% = 1,27 Mio. DM ^{⋅ =} PF r V VaR

VaR

µ = − ⋅ − + ⋅ = % 0898 , 0 %) 1794 , 0 ( ) 36 , 0 ( % 0387 , 0 64 , 0

r PF

σ − ⋅ ⋅ ⋅ − ⋅ ⋅ + ⋅ − + ⋅ = ^{2 2 2 2} ) 5845 , 0 ( % 7807 , 0 % 226 , 0 ) 36 , 0 ( 64 , 0 2 % 7807 , 0 ) 36 , 0 ( % 226 , 0 64 , 0

r PF

= % 3857 , 0

= − ⋅ = % 6662 , 0 % 0898 , 0 % 3857 , 0 2 r

VaR

∑ ⋅ = V r VaR = 190,52 Mio. DM · 0,6662% = 1,27 Mio. DM

n VaR

n

Es zeigt sich, dass beide Verfahren zum gleichen Ergebnis führen.

150 Mio. USD short, europäisch, Strike: 1,40 DM, Restlaufzeit 1 Jahr; Wert am 31.07.1995: 0,0963 / 1 USD; Delta: 0,5119 Der Portfoliowert am 31.07.1995 beträgt 229,1704 Mio. DM. ^{∧ ∧} v T µ ⋅ = ∑ ^⋅ M v T = 0,2035 ; = 0,2034% ^{σ ⋅ =} v

r PF

∧ ∧

∑ µ σ ⋅ − ⋅ = = (1,96 · 0,203400% - 0,0197997%) · 156.350.693 DM V z VaR ) ( ¹ r ^{− α} n N r PF PF

= 592.362 DM

Die Herleitung des Ergebnisses befindet sich im Anhang der Arbeit (S. 19).

In der obigen Darstellung wurden die Marktparameter als konstant unterstellt. Diese Prämisse wird nun aufgegeben und in die Modellierung implementiert. Man unterstellt, dass die Marktparameter einer Normalverteilung folgen. Daraus kann man folgern, dass die Wertänderung der Marktparameter ebenso normalverteilt sind. ²² Λ σ σ σ   µ  

^{ξ ξ ξ ξ ξ ξ ∆ ∆ ∆ ∆ ∆ ∆ ξ ∆ , , ,}     M ^{1 2 1 1 1} 1

Λ σ σ σ µ    

^{ξ ξ ξ ξ ξ ξ ∆ ∆ ∆ ∆ ∆ ∆ , , , ξ ∆} ∑ = M ^{2 2 2 1 2} =   M ²  

^ξ Μ Ο Μ Μ ^{∆ ξ ∆} Μ

;    

    Λ σ σ σ µ

^{ξ ξ ξ ξ ξ ξ ∆ ∆ ∆ ∆ ∆ ∆}   ^{, , , ξ ∆}   M M M M ^{2 1} M

Zuerst muss der Wert der einzelnen Vermögensgegenstände in Abhängigkeit der Marktpara- werden. ξ ξ ξ = ) ,..., , ( V V

^{2 1} M n n

Als nächstes wird ein Marktparameter um einen Basispunkt ausgelenkt und der Wert des Vermögensgegenstandes neu bestimmt. Anschließend wird die Differenz zwischen neuen und alten Wert gebildet. ^ξ ξ ξ ξ ξ ξ ξ − + = Wert eine Basispunktes = ) ,..., ,..., ( ) ),..., ( ,..., ( V bp V BPV m

^{1 1} M m M m n V N

Dies wird für alle Marktparameter wiederholt und für jeden Vermögensgegenstand ein Vektor bestimmt.

^{ξ ξ} = T ) ... ( BPV BPV BPV ¹ M

V V V n n n

Daraus ergibt sich für das Portfolio der Vektor: ⋅ + + ⋅ = BPV U BPV U BPV ... ( U ^N = Einheiten pro Vermögensgegenstand)

V N V PF ^{1 1} N

Damit man den Value at Risk mit der Normalverteilungsannahme berechnen kann, benötigt man den Mittelwert und die Standardabweichung des Portfolios.

∑ ^∆ T µ ⋅ = T ⋅ = σ M BPV BPV BPV

^{∆ ξ} PF PF PF ^{ξ ∆ ∆} PF PF r

σ µ ⋅ − − = ) ( z VaR

^{α ∆ − ∆ 1} PF PF Die theoretischen Ausführungen werden nun mit der Hilfe eines Beispieles erläutert.

Es wird unterstellt, dass die Parameter gemeinsam normalverteilt sind.     % 05 , 5 % 0315 , 0 % 0665 , 0 % 1225 , 0

   

∑ = = % 60 , 7 M und % 0190 , 0 % 0400 , 0 % 0665 , 0    

ξ ξ

   

% 20 , 10 % 0100 , 0 % 0190 , 0 % 0315 , 0     Wie oben erwähnt, sind dann auch die Wertänderungen normalverteilt.     bp 5 bp bp bp 15 , 3 65 , 6 25 , 12

   

∑ = = bp M 10 bp bp bp 9 , 1 4 65 , 6    

^{∆ ξ ξ ∆} und

   

bp 20 bp bp bp 1 9 , 1 15 , 3     Das Portfolio besteht aus U ¹ = -1000 Einheiten einer Anleihe mit 3 Jahren Restlaufzeit und einem Coupon von 15%. Daraus ergibt sich ein Wert von: 115 15 15

= + + = 6669 , 113 V DM

( ) ( ) ¹ + ^{3 2} + + 05 , 0 1 15 , 0 1 1 , 0 1 Das andere Wertpapier besteht aus U ² = 500 Einheiten und ist ein dreijähriger Zerobond. ² = V 1315 , 75 DM

−       6655 , 113 6669 , 113 0014 , 0

     

− = − = BPV 6645 , 113 6669 , 113 0024 , 0      

V , ¹      

− 6433 , 113 6669 , 113 0236 , 0      

      0 1315 , 75 1315 , 75

     

= − = 0 1315 , 75 1315 , 75 BPV      

V

²      

− 0205 , 0 1315 , 75 1110 , 75      

daraus ergibt sich für das Portfolio: −       36 , 1 0 0014 , 0

     

= ⋅ + − − = 41 , 2 0 500 0024 , 0 1000 BPV      

PF

     

− − 32 , 13 0205 , 0 0236 , 0       Daraus kann die Wertänderung des Portfolios berechnet werden:   bp 5

 

µ ⋅ = = DM bp 27 , 297 10 ) 32 , 13 41 , 2 36 , 1 (  

^∆ PF

 

bp 20  

    15 , 3 65 , 6

Daraus berechnet sich der VaR für das 97,5 % Konfidenzintervall: VaR = 1,96 · 503,31 DM - 297,27 DM = 689,22 DM Nähere Herleitungen siehe Anhang (S. 20 / 21)

rer Portfoliostrukturen und bei der Verwendung der Differenzsimulation führen Portfolio- und Faktoransatz zu identischen Ergebnissen. 24

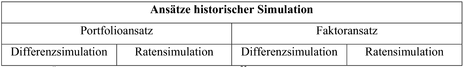
Tabelle 2: Übersicht über Ansätze historischer Simulation ²⁵

Beim Portfolioansatz ermittelt man die Wertänderungen der Vermögensgegenstände, während beim Faktoransatz die Marktfaktoren simuliert werden. Wenn die entsprechenden Value at Risk Marktfaktoren bestimmt sind, lässt sich daraus der Wert der einzelnen Assets berechnen. In der weiteren Ausführung wird nur der Portfolioansatz näher betrachtet, da die Untersuchung des Faktoransatzes den Rahmen der Arbeit überschreiten würde. Neben der Unterscheidung in Faktor- und Portfolioansatz kann man weiter zwischen Differenz- und Ratensimulation unterscheiden. Bei der Differenzsimulation werden nur absolute Wertänderungen betrachtet, wohingegen man bei der Ratensimulation relative Wertänderungen betrachtet. Nachfolgend werden die Differenzsimulation und die Ratensimulation anhand eines numerischen Beispiel erklärt.

Tabelle 3: Historische Simulation

In der ersten Spalte wurden die Aktienkurse der letzten 20 Handelstage abgetragen. Spalte zwei und drei sind für die Berechnung mit der Differenzsimulation nötig. Bei einem 95% Konfidenzintervall determiniert der zweitkleinste Wert den VaR (VaR= 0,52€, d.h. ein Verlust von 0,52€ wird mit einer Wahrscheinlichkeit von 95% nicht überschritten). Bei der Ratensimulation werden zuerst die relativen Änderungen berechnet (Spalte 4): V

= t r

V

⁻ L t Danach werden diese mit den aktuellen Kursen ( 20,22 € ) multipliziert (Spalte 5) und in aufsteigender Form sortiert (Spalte 6). Die Sortierung kann mit Hilfe eines Sortieralgorithmus z.B. mit Excel einfach implementiert werden. Bei 20 Werten und einem Konfidenzintervall von 95% wird der zweite Wert gewählt (hier: V ^VaR =19,71 € ). Um zum Value at Risk zu kommen wird vom aktuellen Kurs der kritische Wert (V ^VaR ) abgezogen (Spalte 7). − = A V V VaR

VaR

Bei mehreren gleichartigen Aktien im Portfolio wird der VaR mit der Anzahl der Aktien mul- Bei unterschiedlichen Vermögensgegenständen kann man den VaR für alle gleichartigen Aktien einzeln berechnen und die Ergebnisse addieren.

Bei der Anwendung der Historischen Simulation zur Bestimmung des VaR wird kein speziel- stochastisches Modell unterlegt wie etwa die Normalverteilungsannahme beim Korrelationsansatz. Im Beispiel wurde die Historische Simulation mit nur 20 Werten durchgeführt. In der Praxis werden meist über 1000 Werte herangezogen ²⁶ . Dies macht deutlich, mit welchem Aufwand die Historische Simulation einhergeht. Bei Portfolios mit z.B. 100 Werten entsteht ein enormer Rechenaufwand. Bei längeren Simulationshorizonten erhöht sich der Aufwand zusätzlich. Mit Hilfe des Bootstrapping-Verfahrens kann der Aufwand insbesondere bei längeren Simulationshorizonten enorm verringert werden. Aus dem Stichprobenumfang mit 1- Tagesbeobachtungen werden bei einem Simulationshorizont von zehn Tagen zufällig zehn

Werte gezogen und addiert. Dadurch wird der Stichprobenumfang künstlich erhöht ohne da- den Aufwand signifikant zu erhöhen. ²⁷

Der Ansatz der Historischen Simulation enthält indirekt die Korrelation zwischen den Assets, da sich der Portfoliowert aus den gegen- oder gleichläufigen Wertentwicklungen der einzelnen Positionen ergibt. ²⁸

bei der Historischen Simulation können auch bei der Monte Carlo Simulation die Wertänderungen der Assets, oder die Veränderungen der Marktparameter simuliert werden. Bei der Simulation mit Marktparametern ergeben sich große Schwierigkeiten in der Hinsicht, dass die einzelnen Marktparameter teilweise hoch korreliert sind. So ist der Tageszinssatz mit dem 1-Monatszinssatz hoch korreliert, während der Tageszinssatz mit dem 10-Jahres Zins nur sehr schwach korreliert ist. ³⁰ Deshalb muss eine multivariate Verteilungsannahme getroffen werden, und nicht für jeden Marktparameter eine isolierte Verteilungsannahme zugrundegelegt werden.

Bei der Monte Carlo Simulation wird zuerst mit Hilfe eines Softwareprogramms ein Menge von Zufallszahlen gezogen (siehe Spalte 2 Tabelle 4). Diese Zufallszahlen haben für die Simulation Ausprägungen zwischen null und eins. Zudem sind sie als Wahrscheinlichkeitswerte der Verteilungsfunktion der Standardnormalverteilung zu betrachten. Eine Zufallszahl von 0,9990 entspricht einem Z-Wert von 3,09. Z-Werte die kleiner als Null sind erhält man für Zufallszahlen die kleiner als 0,5 sind (Spalte 3). Die Z-Werte berechnen sich wie folgt: µ − X

= Z

σ Man löst die Formel nach X auf und ersetzt X durch r um zu stetig normalverteilten Renditen zu gelangen (im Beispiel entspricht dies Spalte 4 Tabelle 4):

µ σ + ⋅ = Z r Danach sind die Ergebnisse zu sortieren (Spalte 5). Nun erscheint es sinnvoll, mit einem Zahlenbeispiel die bisherigen Ausführungen darzustellen.

Betrachtet wird ein Portfolio mit 5.000 Aktien vom Typ X (414€) und 10.000 Aktien vom Typ Y (268,5€). Daraus folgt ein Gesamtwert für das Portfolio von 4.755.000 €. Um die Monte Carlo Simulation mit der Normalverteilungsannahme durchführen zu können, benötigt man den Erwartungswert und die Standardabweichung. Diese beiden Parameter werden aus historischen Erfahrungswerten bestimmt. µ = 0,981447% σ = 7,004843% ;

Tabelle 4: Beispiel zur Monte Carlo Simulation

Im nächsten Schritt führt man eine Gewinn- und Verlustrechnung durch (siehe Tabelle 5).

Tabelle 5: Rangfolge der Gewinne und Verluste in der Monte Carlo Simulation

Die Gewinne und Verluste (Spalte 3 Tabelle 5) berechnet man mit Hilfe von e ^{r i} . Dadurch werden stetige Änderungsraten unterstellt. ³² In diesem Beispiel ergibt sich für ein Konfidenzintervall von 95% ein Value at Risk von 505.600 €.

Abschließend ist zur Monte Carlo Simulation zu sagen, dass sie sehr aufwendig zu implementieren ist. Außerdem ist bei einer nur geringfügigen Änderung des Portfolios der gesamte Rechenaufwand zu wiederholen.

5. Schlussbetrachtung Insgesamt ist festzuhalten, dass die drei vorgestellten Ansätze einen relativ hohen Rechenaufwand benötigen. Es ist deshalb unter ökonomischen Gesichtspunkten zu bestimmen, ob sich der Aufwand für die Berechnung des Value at Risk lohnt, oder ob man nicht auf das Konzept der Standardnormalverteilung zurückgreift. Besonders hervorzuheben ist, dass der Korrelationsansatz und die Monte Carlo Simulation in der Praxis meist unter der Normalverteilungsannahme berechnet werden, obwohl man auch eine andere Verteilung wählen kann. Dabei wurde festgestellt, dass die Normalverteilungsannahme von Renditen grundsätzlich

fundierter ist, als etwa bei absoluten Wertänderungen. Die Normalverteilung ist besonders an den Rändern kritisch, da sie impliziert, dass sowohl unendlich große Verluste oder Gewinne auftreten können. In der Realität kommen in der Mitte zudem höhere Werte vor. In der Literatur wird deshalb diskutiert die Normalverteilung durch die Lognormalverteilung oder die t-Verteilung zu ersetzten. Da bisher nicht geklärt werden konnte, welche Verteilung zur VaR Berechnung optimal ist, muss das Verfahren kritisch gesehen werden. Daher soll das Konzept auch nur eine Ergänzung im Risikomanagementprozess darstellen und nur als eine Möglichkeit zur Risikoquantifizierung betrachtet werden. Ob und wie das Verfahren in der betrieblichen Praxis eingesetzt wird, muss fallspezifisch ermittelt werden. Oft werden im Betrieb die Risiken subjektiv von den entsprechenden Entscheidungsträgern geschätzt, da dies weniger aufwendig ist und besonders bei kleiner empirischer Datenbasis zu besseren Ergebnissen führen kann. ³³